题目内容
【题目】在四棱锥![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,且
,且![]() ,
, ![]() 为线段
为线段![]() 上一点.
上一点.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 且
且![]() ,求证:
,求证: ![]() 平面
平面![]() ,并求四棱锥
,并求四棱锥![]() 的体积.
的体积.
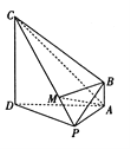
【答案】(1)见解析(2)5
【解析】试题分析:(1)证明面面垂直可证线面垂直,因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,所以
,所以![]() ,又
,又![]() ,且
,且![]() ,所以
,所以![]() 平面
平面![]() .(2)在
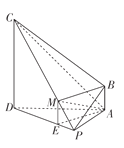
.(2)在![]() 上取一点
上取一点![]() ,使得
,使得![]() ,因为
,因为![]() ,所以
,所以![]() .又
.又![]() ,所以
,所以![]() ,所以四边形
,所以四边形![]() 为平行四边形,因为
为平行四边形,因为![]() 平面
平面![]() ,所以
,所以![]() .因为
.因为![]() ,
, ![]() ,即点
,即点![]() 到
到![]() 的距离为
的距离为![]() ,再根据椎体体积公式求解即可
,再根据椎体体积公式求解即可
试题解析:
证明:(1)因为![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() ,又
,又![]() ,且
,且![]() ,所以
,所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)在![]() 上取一点
上取一点![]() ,使得
,使得![]() ,
,
因为![]() ,所以
,所以![]() .
.
又![]() ,所以
,所以![]() ,
,
所以四边形![]() 为平行四边形,
为平行四边形,
所以![]() ,又
,又![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,
,
所以![]() 平面
平面![]() .
.
因为![]() 平面
平面![]() ,所以
,所以![]() .因为
.因为![]() ,
, ![]() ,即点
,即点![]() 到
到![]() 的距离为
的距离为![]() ,
,
即得点![]() 到平面
到平面![]() 的距离为2,
的距离为2,
![]() ,所以点
,所以点![]() 到平面
到平面![]() 的距离为
的距离为![]() ,
,
所以![]()
![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 | 1 | 2 | 3 |
利润 | 2 | 3.9 | 5.5 |
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测4月和5月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过1000万?
相关公式: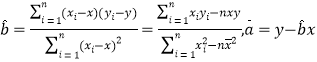 .
.