题目内容
【题目】已知关于的不等式![]() 的解集为
的解集为![]() ;
;
(1)若![]() ,求
,求![]() 的取值范围;
的取值范围;
(2)若存在两个不相等负实数![]() 、
、![]() ,使得
,使得![]() ,求实数
,求实数![]() 的取值范围;
的取值范围;
(3)是否存在实数![]() ,满足:“对于任意
,满足:“对于任意![]() ,都有
,都有![]() ,对于任意的
,对于任意的![]() ,都有
,都有![]() ”,若存在,求出
”,若存在,求出![]() 的值,若不存在,说明理由.
的值,若不存在,说明理由.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在,
;(3)存在,![]()
【解析】
(1)讨论二次项系数![]() 和不等于0两种情况,当不等式的解集为
和不等于0两种情况,当不等式的解集为![]() 时,
时,![]() 的取值范围;(2)根据不等式的解集形式可知
的取值范围;(2)根据不等式的解集形式可知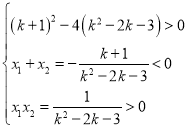 ,求
,求![]() 的范围;(3)根据题意判断不等式的解集
的范围;(3)根据题意判断不等式的解集![]() ,讨论
,讨论![]() 的情况,根据不等式的解集情况判断是否存在.
的情况,根据不等式的解集情况判断是否存在.
(1)当![]() 时,
时,![]() 或
或![]()
当![]() 时,
时,![]() 恒成立,
恒成立,
当![]() 时,
时,![]() 不恒成立,舍去,
不恒成立,舍去,
当![]() 时,
时,
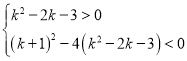
解得![]() 或
或![]() ,
,
综上可知![]() 或
或![]() ;
;
(2)根据不等式解集的形式可知![]() 或
或![]() ,
,
![]() 不等式解集的两个端点就是对应方程的实数根,
不等式解集的两个端点就是对应方程的实数根,
即![]() 有两个不相等的负根,
有两个不相等的负根,
即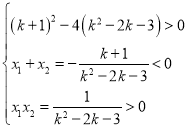 ,解得
,解得![]() ,
,
综上可知:![]() ;
;
(3)根据题意可知,得出解集![]() ,
,![]() ,
,
当![]() 时,解得
时,解得![]() 或
或![]() ,
,
当![]() 时,
时,![]() 恒成立,不满足条件,
恒成立,不满足条件,
当![]() 时,不等式的解集是
时,不等式的解集是![]() ,满足条件;
,满足条件;
当![]() 时,此时一元二次不等式的解集形式不是
时,此时一元二次不等式的解集形式不是![]() 的形式,不满足条件;
的形式,不满足条件;
当![]() 时,此时一元二次不等式的解集形式不是
时,此时一元二次不等式的解集形式不是![]() 的形式,不满足条件;
的形式,不满足条件;
综上,满足条件的![]() 的值为3.
的值为3.

练习册系列答案
相关题目