题目内容
【题目】已知D=  ,给出下列四个命题:
,给出下列四个命题:
P1:(x,y)∈D,x+y+1≥0;
P2:(x,y)∈D,2x﹣y+2≤0;
P3:(x,y)∈D, ![]() ≤﹣4;
≤﹣4;
P4:(x,y)∈D,x2+y2≤2.
其中真命题的是( )
A.P1 , P2
B.P2 , P3
C.P2 , P4
D.P3 , P4
【答案】C
【解析】解:不等式组 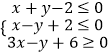 的可行域如图,
的可行域如图,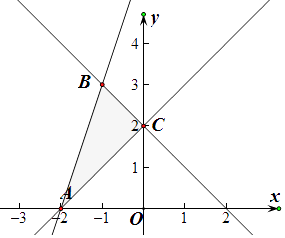
p1:A(﹣2,0)点,﹣2+0+1=﹣1,
故(x,y)∈D,x+y≥0为假命题;
p2:A(﹣1,3)点,﹣2﹣3+2=﹣3,
故(x,y)∈D,2x﹣y+2≤0为真命题;
p3:C(0,2)点, ![]() =﹣3,
=﹣3,
故(x,y)∈D, ![]() ≤﹣4为假命题;
≤﹣4为假命题;
p4:(﹣1,1)点,x2+y2=2
故(x,y)∈D,x2+y2≤2为真命题.
可得选项p2 , p4正确.
故选:C.
【考点精析】解答此题的关键在于理解二元一次不等式(组)所表示的平面区域的相关知识,掌握不等式组表示的平面区域是各个不等式所表示的平面区域的公共部.

练习册系列答案
相关题目

