题目内容
【题目】已知函数f(x)=2lnx+ax﹣ ![]() (a∈R)在x=2处的切线经过点(﹣4,2ln2)
(a∈R)在x=2处的切线经过点(﹣4,2ln2)
(1)讨论函数f(x)的单调性
(2)若不等式 ![]() 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
【答案】
(1)解:由f(x)=2lnx+ax﹣ ![]() (a∈R),求导f′(x)=
(a∈R),求导f′(x)= ![]() +a+
+a+ ![]() ,
,
当x=2时,f′(2)=1+a+f′(2),
∴a=﹣1,
设切点为(2,2ln2+2a﹣2f′(2)),则切线方程y﹣(2ln2+2a﹣2f′(2))=f′(2)(x﹣2),
将(﹣4,2ln2)代入切线方程,2ln2﹣2ln2﹣2a+2f′(2))=﹣6f′(2),则f′(2)=﹣ ![]() ,
,
∴f′(x)= ![]() ﹣1﹣
﹣1﹣ ![]() =
= ![]() ≤0,
≤0,
∴f(x)在(0,+∞)单调递减
(2)解:由不等式 ![]() 恒成立,则
恒成立,则 ![]() (2lnx+
(2lnx+ ![]() )>m,
)>m,
令φ(x)=2lnx+ ![]() ,(x>0)求导φ′(x)=
,(x>0)求导φ′(x)= ![]() ﹣
﹣ ![]() ﹣1=﹣(
﹣1=﹣( ![]() ﹣1)2≤0,
﹣1)2≤0,
∴φ(x)在(0,+∞)单调递减,
由φ(1)=0,
则当0<x<1时,φ(x)>0,
当x>1时,φ(x)<0,
∴ ![]() (2lnx+
(2lnx+ ![]() )在(0,+∞)恒大于0,
)在(0,+∞)恒大于0,
∴m≤0,
实数m的取值范围(﹣∞,0]
【解析】(1)求导,当x=2时,代入f′(x),即可求得a=﹣1,求得点斜式方程,将(﹣4,2ln2)代入点斜式方程,即可求得f′(2),即可求得函数f(x)的单调区间;(2)由题意可知 ![]() (2lnx+
(2lnx+ ![]() )>m,构造辅助函数,求导,根据函数的单调性及零点性质,求得
)>m,构造辅助函数,求导,根据函数的单调性及零点性质,求得 ![]() (2lnx+
(2lnx+ ![]() )最小值,即可求得实数m的取值范围.
)最小值,即可求得实数m的取值范围.
【考点精析】本题主要考查了利用导数研究函数的单调性和函数的最大(小)值与导数的相关知识点,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减;求函数
在这个区间单调递减;求函数![]() 在
在![]() 上的最大值与最小值的步骤:(1)求函数
上的最大值与最小值的步骤:(1)求函数![]() 在
在![]() 内的极值;(2)将函数
内的极值;(2)将函数![]() 的各极值与端点处的函数值
的各极值与端点处的函数值![]() ,
,![]() 比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.
比较,其中最大的是一个最大值,最小的是最小值才能正确解答此题.

【题目】![]() 某公司为了了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据 用户对其产品的满意度的评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频率分布表.A地区用户满意度评分的频率分布直方图
某公司为了了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据 用户对其产品的满意度的评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频率分布表.A地区用户满意度评分的频率分布直方图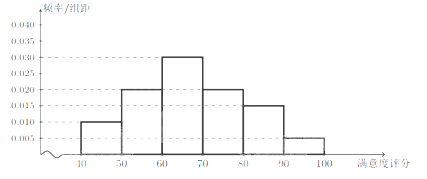
B地区用户满意度评分的频率分布表
满意度评分分组 | [50,60) | [50,60) | [50,60) | [50,60) | [50,60) |
频数 | 2 | 8 | 14 | 10 | 6 |
(1)(I)在答题卡上作出B地区用户满意度评分的频率分布直方图,并通过此图比较两地区满意度评分的平均值及分 散 程度.(不要求计算出具体值,给出结论即可)
B地区用户满意度评分的频率分布直方图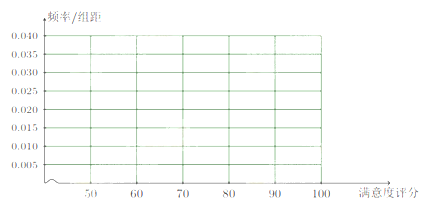
(2)(II)根据用户满意度评分,将用户的满意度评分分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
估计那个地区的用户的满意度等级为不满意的概率大,说明理由.
