题目内容
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴,且两个坐标系取相等的长度单位,已知直线l的参数方程为 ![]() (t为参数,0<φ<π),曲线C的极坐标方程为ρcos2θ=8sinθ.
(t为参数,0<φ<π),曲线C的极坐标方程为ρcos2θ=8sinθ.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)设直线l与曲线C相交于A、B两点,当φ变化时,求|AB|的最小值.
【答案】
(1)解:直线l的参数方程为 ![]() 消去参数可得:xcosφ﹣ysinφ+2sinφ=0;
消去参数可得:xcosφ﹣ysinφ+2sinφ=0;
即直线l的普通方程为xcosφ﹣ysinφ+2sinφ=0;
曲线C的极坐标方程为ρcos2θ=8sinθ.可得:ρ2cos2θ=8ρsinθ.
那么:x2=8y.
∴曲线C的直角坐标方程为x2=8y
(2)解:直线l的参数方程带入C的直角坐标方程,可得:t2cos2φ﹣8tsinφ﹣16=0;
设A,B两点对应的参数为t1,t2,
则 ![]() ,
, ![]() .
.
∴|AB|=|t1﹣t2|= ![]() =
= ![]() .
.
当φ= ![]() 时,|AB|取得最小值为8
时,|AB|取得最小值为8
【解析】(1)直接消去直线l的参数可得普通方程;根据ρcosθ=x,ρsinθ=y,ρ2=x2+y2 , 进行代换即得曲线C的直角坐标方程.(2)将直线l的参数方程带入C的直角坐标方程;设出A,B两点的参数,利用韦达定理建立关系求解最值即可.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案【题目】![]() 某公司为了了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据 用户对其产品的满意度的评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频率分布表.A地区用户满意度评分的频率分布直方图
某公司为了了解用户对其产品的满意度,从A,B两地区分别随机调查了40个用户,根据 用户对其产品的满意度的评分,得到A地区用户满意度评分的频率分布直方图和B地区用户满意度评分的频率分布表.A地区用户满意度评分的频率分布直方图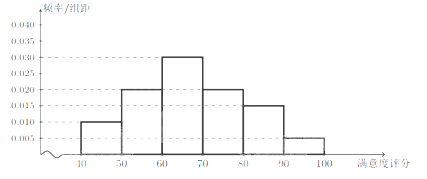
B地区用户满意度评分的频率分布表
满意度评分分组 | [50,60) | [50,60) | [50,60) | [50,60) | [50,60) |
频数 | 2 | 8 | 14 | 10 | 6 |
(1)(I)在答题卡上作出B地区用户满意度评分的频率分布直方图,并通过此图比较两地区满意度评分的平均值及分 散 程度.(不要求计算出具体值,给出结论即可)
B地区用户满意度评分的频率分布直方图
(2)(II)根据用户满意度评分,将用户的满意度评分分为三个等级:
满意度评分 | 低于70分 | 70分到89分 | 不低于90分 |
满意度等级 | 不满意 | 满意 | 非常满意 |
估计那个地区的用户的满意度等级为不满意的概率大,说明理由.
