题目内容
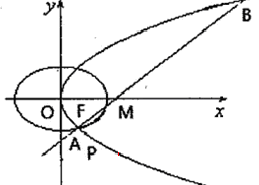
已知抛物线C: 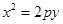 的焦点为F,
的焦点为F,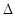 ABQ的三个顶点都在抛物线C上,点M为AB的中点,
ABQ的三个顶点都在抛物线C上,点M为AB的中点,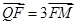 .(1)若M
.(1)若M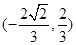 ,求抛物线C方程;(2)若
,求抛物线C方程;(2)若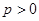 的常数,试求线段
的常数,试求线段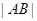 长的最大值.
长的最大值.
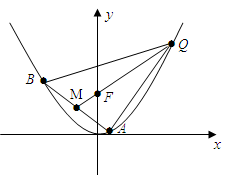
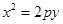 的焦点为F,
的焦点为F,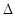 ABQ的三个顶点都在抛物线C上,点M为AB的中点,
ABQ的三个顶点都在抛物线C上,点M为AB的中点,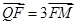 .(1)若M
.(1)若M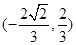 ,求抛物线C方程;(2)若
,求抛物线C方程;(2)若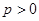 的常数,试求线段
的常数,试求线段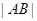 长的最大值.
长的最大值.
(1)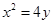 ,(2)
,(2)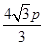 .
.
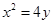 ,(2)
,(2)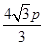 .
.试题分析:(1)本小题中设
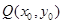 ,又
,又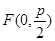 ,而
,而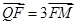 转化为坐标关系,从而可求出Q点坐标(含P),又Q点在抛物线上,所以代入Q点坐标可求得P;(2)本小题中可设直线AB的方程为
转化为坐标关系,从而可求出Q点坐标(含P),又Q点在抛物线上,所以代入Q点坐标可求得P;(2)本小题中可设直线AB的方程为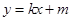 及
及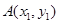 ,
,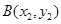 ,
,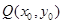 ,联立
,联立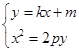 消y,得到关于x的一元二次方程(其中
消y,得到关于x的一元二次方程(其中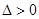 可得m的取值范围),而
可得m的取值范围),而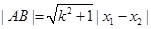 ,则根据韦达定理,可写出
,则根据韦达定理,可写出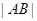 关于m的函数关系,从而求出其最大值.
关于m的函数关系,从而求出其最大值.试题解析:(1)由题意
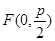 ,设
,设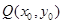 ,因为M
,因为M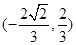 ,
,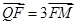 。所以
。所以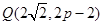 ,代人
,代人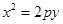 得p=2或p=-1.由题意M在抛物线内部,所以
得p=2或p=-1.由题意M在抛物线内部,所以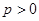 ,故抛物线C:
,故抛物线C: 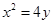 .
.(2)设直线AB的方程为
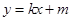 ,点
,点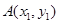 ,
,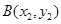 ,
,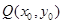 .由
.由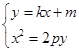 得
得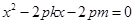 ,于是
,于是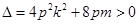 ,
,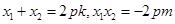 ,所以AB中点M的坐标为
,所以AB中点M的坐标为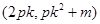 ,由
,由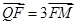 ,得
,得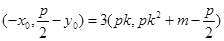 ,所以
,所以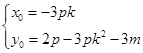 ,由
,由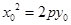 得
得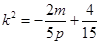 ,由
,由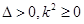 ,得
,得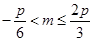 ,又因为
,又因为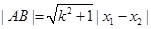 =2
=2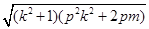 =2
=2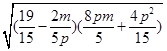 =
=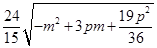 ,记
,记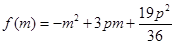
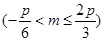 ,易得
,易得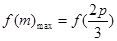 =
=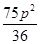 ,所以
,所以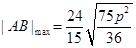 =
=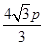 .
.
练习册系列答案
 智慧小复习系列答案
智慧小复习系列答案
相关题目
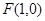 ,直线
,直线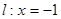 ,动点P到点F的距离与到直线
,动点P到点F的距离与到直线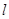 的距离相等.
的距离相等.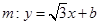 与曲线C交于A,B两点,若曲线C上存在点D使得四边形FABD为平行四边形,求b的值.
与曲线C交于A,B两点,若曲线C上存在点D使得四边形FABD为平行四边形,求b的值. 的抛物线方程为 .
的抛物线方程为 . 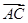 ·
· =0,设P为弦AB的中点.
=0,设P为弦AB的中点.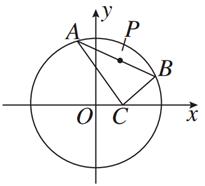
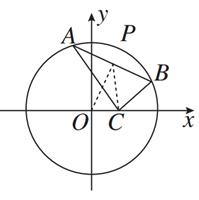
 ,求直线l的方程;
,求直线l的方程;