题目内容
已知点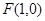 ,直线
,直线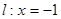 ,动点P到点F的距离与到直线
,动点P到点F的距离与到直线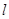 的距离相等.
的距离相等.
(1)求动点P的轨迹C的方程;(2)直线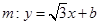 与曲线C交于A,B两点,若曲线C上存在点D使得四边形FABD为平行四边形,求b的值.
与曲线C交于A,B两点,若曲线C上存在点D使得四边形FABD为平行四边形,求b的值.
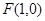 ,直线
,直线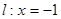 ,动点P到点F的距离与到直线
,动点P到点F的距离与到直线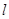 的距离相等.
的距离相等.(1)求动点P的轨迹C的方程;(2)直线
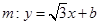 与曲线C交于A,B两点,若曲线C上存在点D使得四边形FABD为平行四边形,求b的值.
与曲线C交于A,B两点,若曲线C上存在点D使得四边形FABD为平行四边形,求b的值.(1)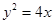 ;(2)
;(2)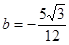 或
或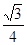 。
。
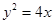 ;(2)
;(2)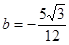 或
或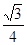 。
。 试题分析:(1)显然动点
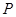 的轨迹满足抛物线的定义,故用定义去求轨迹方程;(2)法一:由题意知
的轨迹满足抛物线的定义,故用定义去求轨迹方程;(2)法一:由题意知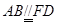 ,
,故设直线FD的方程为
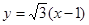 ,与抛物线方程联立可得
,与抛物线方程联立可得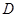 点的横坐标,再由抛物线的定义求出
点的横坐标,再由抛物线的定义求出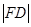 ,
,把直线
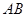 的方程与抛物线方程联立,再由弦长公式求出
的方程与抛物线方程联立,再由弦长公式求出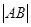 的长,是用
的长,是用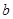 来表示的,然后令
来表示的,然后令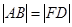
可得关于
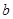 的方程,从而求出
的方程,从而求出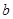 的值;法二:同法一一样先求出
的值;法二:同法一一样先求出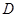 点的坐标,再把直线
点的坐标,再把直线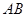 的方程与抛物
的方程与抛物线方程联立,利用韦达定理求出
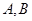 两点的横坐标和与积, 又因为四边形FABD是平行四边形,所以
两点的横坐标和与积, 又因为四边形FABD是平行四边形,所以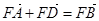 ,由此可得
,由此可得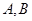 两点的横坐标的关系,结合韦达定理得到的结论找到一个关于
两点的横坐标的关系,结合韦达定理得到的结论找到一个关于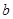 的方程,
的方程,解方程即可,需根据
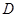 点的坐标进行分情况讨论。
点的坐标进行分情况讨论。试题解析:(1)依题意,动点P的轨迹C是以
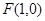 为焦点,
为焦点,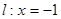 为准线的抛物线,
为准线的抛物线, 所以动点P的轨迹C的方程为
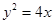
(2)解法一:因为
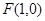 ,故直线FD的方程为
,故直线FD的方程为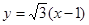 ,
, 联立方程组
 消元得:
消元得: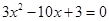 ,
,解得
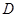 点的横坐标为
点的横坐标为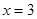 或
或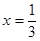 , 由抛物线定义知
, 由抛物线定义知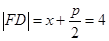 或
或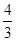
又由
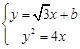 消元得:
消元得: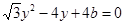 。
。设
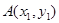 ,
,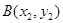 ,则
,则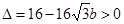 且
且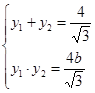 ,
,所以
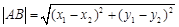
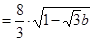
因为FABD为平行四边形,所以
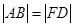 所以
所以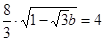 或
或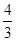 ,
,解得
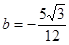 或
或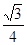 ,代入
,代入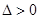 成立。
成立。(2)解法二:因为
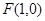 ,故直线FD的方程为
,故直线FD的方程为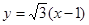
联立方程组
 消元得:
消元得: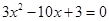 ,解得
,解得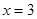 或
或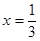
故点
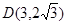 或
或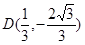 .
. 1)当
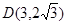 时,设
时,设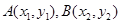 ,
,联立方程组
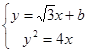 消元得
消元得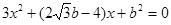 (*)
(*) 根据韦达定理有
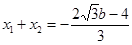 ①,
①, 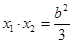 ②
② 又因为四边形是平行四边形,所以
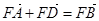 ,将坐标代入有
,将坐标代入有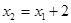 ③
③ 代入①有
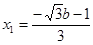 ,
,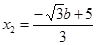 ,再代入②有
,再代入②有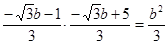
整理得
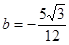 此时(*)的判别式
此时(*)的判别式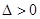 ,符合题意.
,符合题意. 2)当
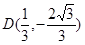 时,同理可解得
时,同理可解得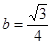 。
。
练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
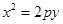 的焦点为F,
的焦点为F,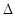 ABQ的三个顶点都在抛物线C上,点M为AB的中点,
ABQ的三个顶点都在抛物线C上,点M为AB的中点,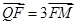 .(1)若M
.(1)若M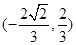 ,求抛物线C方程;(2)若
,求抛物线C方程;(2)若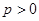 的常数,试求线段
的常数,试求线段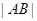 长的最大值.
长的最大值.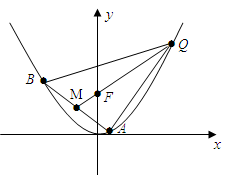
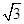 的直线与L相交于A,与C的一个交点为B,若
的直线与L相交于A,与C的一个交点为B,若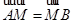 ,则p=____ 。
,则p=____ 。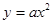 的焦点为
的焦点为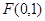 ,则
,则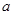 的值为( )
的值为( ) 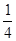
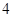
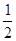
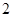
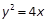 上的一点,F为抛物线的焦点,A在圆C:
上的一点,F为抛物线的焦点,A在圆C: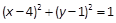 上,则
上,则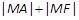 的最小值为__________.
的最小值为__________.