题目内容
双曲线
-y2=1,(n>1)的两焦点为F1、F2,P在双曲线上,且满足|PF1|+|PF2|=2
,则△PF1F2的面积为( )
| x2 |
| n |
| n+2 |
A.
| B.1 | C.2 | D.4 |
不妨设F1、F2是双曲线的左右焦点,
P为右支上一点,
|PF1|-|PF2|=2
①
|PF1|+|PF2|=2
②,
由①②解得:
|PF1|=
+
,|PF2|=
-
,
得:|PF1|2+|PF2|2=4n+4=|F1F2|2,
∴PF1⊥PF2,
又由①②分别平方后作差得:
|PF1||PF2|=2,
故选B
P为右支上一点,
|PF1|-|PF2|=2
| n |
|PF1|+|PF2|=2
| n+2 |
由①②解得:
|PF1|=
| n+2 |
| n |
| n+2 |
| n |
得:|PF1|2+|PF2|2=4n+4=|F1F2|2,
∴PF1⊥PF2,
又由①②分别平方后作差得:
|PF1||PF2|=2,
故选B

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
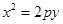 的焦点为F,
的焦点为F,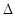 ABQ的三个顶点都在抛物线C上,点M为AB的中点,
ABQ的三个顶点都在抛物线C上,点M为AB的中点,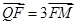 .(1)若M
.(1)若M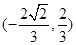 ,求抛物线C方程;(2)若
,求抛物线C方程;(2)若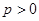 的常数,试求线段
的常数,试求线段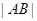 长的最大值.
长的最大值.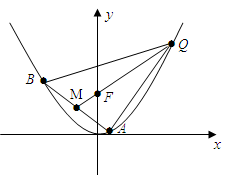
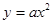 的焦点为
的焦点为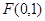 ,则
,则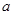 的值为( )
的值为( ) 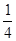
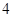
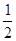
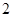
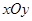 中,点
中,点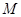 到点
到点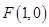 的距离比它到
的距离比它到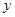 轴的距离多1,记点
轴的距离多1,记点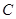 .
.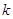 的直线
的直线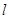 过定点
过定点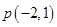 ,求直线
,求直线