题目内容
已知直线x=3与双曲线C:
-
=1的渐近线交于E1,E2两点,记
=
,
=
,任取双曲线上的点P,若
=a
+b
(a,b∈R),则下列关于a,b的表述:
①4ab=1②0<a2+b2<
③a2+b2≥1④a2+b2≥
⑤ab=1
其中正确的是______.
| x2 |
| 9 |
| y2 |
| 4 |
| OE1 |
| e1 |
| OE2 |
| e2 |
| OP |
| e1 |
| e2 |
①4ab=1②0<a2+b2<
| 1 |
| 2 |
| 1 |
| 2 |
其中正确的是______.
双曲线C:
-
=1的渐近线方程为y=±
x,
将直线x=3代入y=±
x,可得E1(3,2),E2(3,-2).
∵
=
,
=
,
∴
=(3,2),
=(3,-2),
∴
=a
+b
=(3a+3b,2a-2b),
∴P(3a+3b,2a-2b),
∵P是双曲线C:
-
=1的点,
∴
-
=1,
∴(a+b)2-(a-b)2=1,
∴4ab=1,∴①正确;
∵a2+b2≥2ab=
,∴④正确;
故答案为:①④.
| x2 |
| 9 |
| y2 |
| 4 |
| 2 |
| 3 |
将直线x=3代入y=±
| 2 |
| 3 |
∵
| OE1 |
| e1 |
| OE2 |
| e2 |
∴
| e1 |
| e2 |
∴
| OP |
| e1 |
| e2 |
∴P(3a+3b,2a-2b),
∵P是双曲线C:
| x2 |
| 9 |
| y2 |
| 4 |
∴
| (3a+3b)2 |
| 9 |
| (2a-2b)2 |
| 4 |
∴(a+b)2-(a-b)2=1,
∴4ab=1,∴①正确;
∵a2+b2≥2ab=
| 1 |
| 2 |
故答案为:①④.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
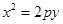 的焦点为F,
的焦点为F, ABQ的三个顶点都在抛物线C上,点M为AB的中点,
ABQ的三个顶点都在抛物线C上,点M为AB的中点,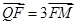 .(1)若M
.(1)若M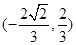 ,求抛物线C方程;(2)若
,求抛物线C方程;(2)若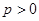 的常数,试求线段
的常数,试求线段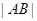 长的最大值.
长的最大值.