题目内容
双曲线x2-y2=1的一弦中点为（2，1），则此弦所在的直线的方程为（ ）
| A．y=2x-1 | B．y=2x-2 | C．y=2x-3 | D．y=2x+3 |
设以A（2，1）为中点的弦两端点为P1（x1，y1），P2（x2，y2），
则x1+x2=4，y1+y2=2．
又x12-y12=1，①
x22-y22=1，②
①-②得：（x1+x2）（x1-x2）=（y1+y2）（y1-y2），
又据对称性知x1≠x2，
∴A（2，1）为中点的弦所在直线的斜率k=2，
∴中点弦所在直线方程为y-1=2（x-2），即y=2x-3．
故选C．
则x1+x2=4，y1+y2=2．
又x12-y12=1，①
x22-y22=1，②
①-②得：（x1+x2）（x1-x2）=（y1+y2）（y1-y2），
又据对称性知x1≠x2，
∴A（2，1）为中点的弦所在直线的斜率k=2，
∴中点弦所在直线方程为y-1=2（x-2），即y=2x-3．
故选C．
练习册系列答案
相关题目
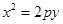的焦点为F，
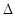ABQ的三个顶点都在抛物线C上，点M为AB的中点，
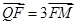.（1）若M
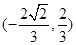，求抛物线C方程；（2）若
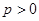的常数，试求线段
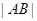长的最大值.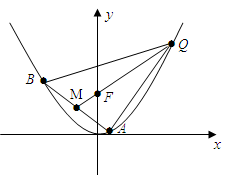
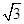的直线与L相交于A，与C的一个交点为B，若
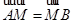，则p=____ 。
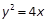上的一点，F为抛物线的焦点，A在圆C:
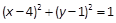上，则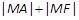
的最小值为__________．
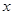＝－2y2的准线方程是 .