题目内容
已知椭圆C1和抛物线C2有公共焦点F(1,0),C1的中心和C2的顶点都在坐标原点,过点M(4,0)的直线l与抛物线C2分别相交于A ,B两点.
(1)如图所示,若 ,求直线l的方程;
,求直线l的方程;
(2)若坐标原点O关于直线l的对称点P在抛物线C2上,直线l与椭圆C1有公共点,求椭圆C1的长轴长的最小值.
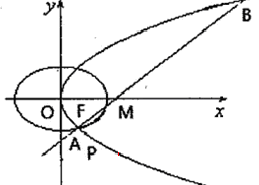
(1)如图所示,若
 ,求直线l的方程;
,求直线l的方程;(2)若坐标原点O关于直线l的对称点P在抛物线C2上,直线l与椭圆C1有公共点,求椭圆C1的长轴长的最小值.

(1)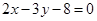 ;(2)长轴长的最小值为
;(2)长轴长的最小值为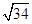 .
.
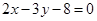 ;(2)长轴长的最小值为
;(2)长轴长的最小值为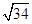 .
.试题分析:(1)首先求得抛物线方程为
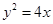 .
.设直线方程为
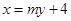 ,并设
,并设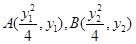
利用
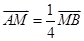 ,得到
,得到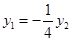 ;
;联立
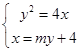 ,可得
,可得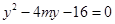 ,应用韦达定理得到
,应用韦达定理得到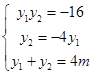 ,
,从而得到
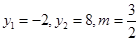 ,求得直线方程.
,求得直线方程.(2)可求得对称点
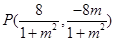 ,
, 代入抛物线中可得:
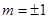 ,直线
,直线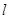 方程为
方程为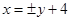 ,考虑到对称性不妨取
,考虑到对称性不妨取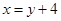 ,
,椭圆设为
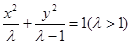 联立直线、椭圆方程并消元整理可得
联立直线、椭圆方程并消元整理可得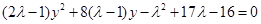 ,
, 由
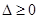 ,可得
,可得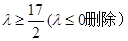 ,即得解.
,即得解.(1)由题知抛物线方程为
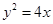 。 2分
。 2分设直线方程为
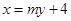 ,并设
,并设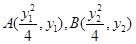
因为
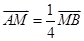 ,所以
,所以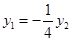 .
.联立
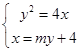 ,可得
,可得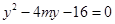 ,有
,有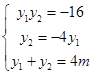 4分
4分解得:
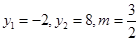 ,所以直线方程为:
,所以直线方程为: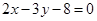 6分
6分 (2)可求得对称点
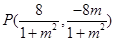 , 8分
, 8分代入抛物线中可得:
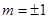 ,直线
,直线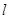 方程为
方程为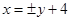 ,考虑到对称性不妨取
,考虑到对称性不妨取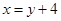 ,
,设椭圆方程为
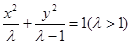 ,联立直线方程和椭圆方程并消元整理得
,联立直线方程和椭圆方程并消元整理得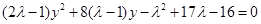 , 10分
, 10分因为椭圆与直线有交点,所以
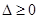 ,
,即:
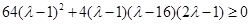 ,解得
,解得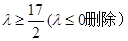 12分
12分即
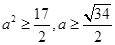
∴长轴长的最小值为
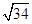 .. 13分
.. 13分
练习册系列答案
相关题目
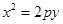 的焦点为F,
的焦点为F,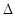 ABQ的三个顶点都在抛物线C上,点M为AB的中点,
ABQ的三个顶点都在抛物线C上,点M为AB的中点,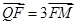 .(1)若M
.(1)若M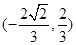 ,求抛物线C方程;(2)若
,求抛物线C方程;(2)若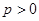 的常数,试求线段
的常数,试求线段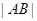 长的最大值.
长的最大值.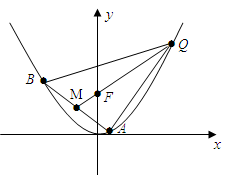
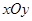 中,点
中,点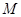 到点
到点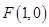 的距离比它到
的距离比它到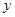 轴的距离多1,记点
轴的距离多1,记点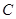 .
.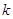 的直线
的直线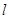 过定点
过定点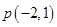 ,求直线
,求直线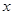 =-2y2的准线方程是 .
=-2y2的准线方程是 .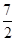 ,4),则|PA|+|PM|的最小值是( )
,4),则|PA|+|PM|的最小值是( )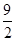
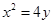 的焦点坐标为 .
的焦点坐标为 .