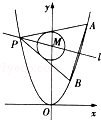
题目内容
已知点C(1,0),点A、B是⊙O:x2+y2=9上任意两个不同的点,且满足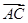 ·
· =0,设P为弦AB的中点.
=0,设P为弦AB的中点.
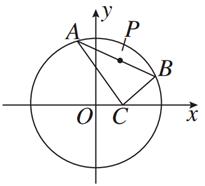
(1)求点P的轨迹T的方程;
(2)试探究在轨迹T上是否存在这样的点:它到直线x=-1的距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.
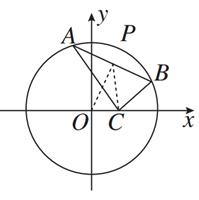
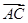 ·
· =0,设P为弦AB的中点.
=0,设P为弦AB的中点.
(1)求点P的轨迹T的方程;
(2)试探究在轨迹T上是否存在这样的点:它到直线x=-1的距离恰好等于到点C的距离?若存在,求出这样的点的坐标;若不存在,说明理由.

(1)x2-x+y2=4
(2)存在,(1,-2)和(1,2)
(2)存在,(1,-2)和(1,2)
(1)连接CP、OP,由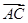 ·
· =0,知AC⊥BC,
=0,知AC⊥BC,
∴|CP|=|AP|=|BP|=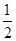 |AB|.
|AB|.
由垂径定理知|OP|2+|AP|2=|OA|2,
即|OP|2+|CP|2=9.
设点P(x,y),有(x2+y2)+[(x-1)2+y2]=9,
化简,得到x2-x+y2=4.
(2)根据抛物线的定义,到直线x=-1的距离等于到点C(1,0)的距离的点都在抛物线y2=2px上,其中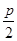 =1,
=1,
∴p=2,故抛物线方程为y2=4x.
由方程组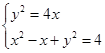 ,得x2+3x-4=0,
,得x2+3x-4=0,
解得x1=1,x2=-4,由于x≥0,
故取x=1,此时y=±2.
故满足条件的点存在,其坐标为(1,-2)和(1,2).
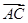 ·
· =0,知AC⊥BC,
=0,知AC⊥BC,∴|CP|=|AP|=|BP|=
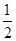 |AB|.
|AB|.由垂径定理知|OP|2+|AP|2=|OA|2,
即|OP|2+|CP|2=9.
设点P(x,y),有(x2+y2)+[(x-1)2+y2]=9,
化简,得到x2-x+y2=4.
(2)根据抛物线的定义,到直线x=-1的距离等于到点C(1,0)的距离的点都在抛物线y2=2px上,其中
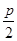 =1,
=1,∴p=2,故抛物线方程为y2=4x.
由方程组
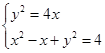 ,得x2+3x-4=0,
,得x2+3x-4=0,解得x1=1,x2=-4,由于x≥0,
故取x=1,此时y=±2.
故满足条件的点存在,其坐标为(1,-2)和(1,2).

练习册系列答案
相关题目
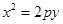 的焦点为F,
的焦点为F,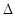 ABQ的三个顶点都在抛物线C上,点M为AB的中点,
ABQ的三个顶点都在抛物线C上,点M为AB的中点,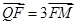 .(1)若M
.(1)若M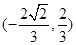 ,求抛物线C方程;(2)若
,求抛物线C方程;(2)若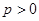 的常数,试求线段
的常数,试求线段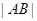 长的最大值.
长的最大值.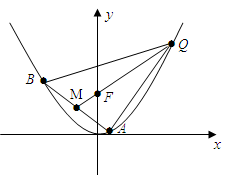
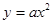 的焦点为
的焦点为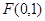 ,则
,则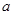 的值为( )
的值为( ) 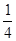
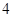
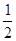
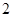
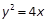 上的一点,F为抛物线的焦点,A在圆C:
上的一点,F为抛物线的焦点,A在圆C: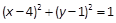 上,则
上,则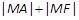 的最小值为__________.
的最小值为__________.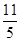
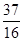
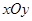 中,点
中,点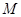 到点
到点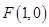 的距离比它到
的距离比它到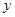 轴的距离多1,记点
轴的距离多1,记点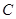 .
.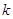 的直线
的直线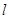 过定点
过定点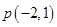 ,求直线
,求直线