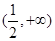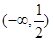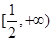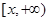题目内容
函数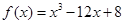 在区间
在区间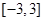 上的最大值与最小值分别为
上的最大值与最小值分别为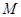 、
、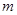 ,则
,则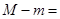 .
.
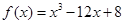 在区间
在区间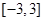 上的最大值与最小值分别为
上的最大值与最小值分别为 、
、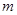 ,则
,则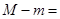 .
.32
试题分析:求出函数的导数,研究出函数在区间[-1,3]上的单调性,确定出函数最值的位置,求出函数的最值,再求M-m.解:∵函数f(x)=x3-12x+8,∴f′(x)=3x2-12,令f′(x)>0,解得x>2或x<-2,故函数在[-3,2]上是减函数,在[2,3]上是增函数,所以函数在x=2时取到最大值24,由于f(2)=-8,f(3)=-1,故函数的最大值是24,则M-m=32,故答案为32.
点评:本题考查函数的最值及其几何意义,解答本题关键是研究出函数的单调性,利用函数的单调性确定出函数的最值,

练习册系列答案
 小学夺冠AB卷系列答案
小学夺冠AB卷系列答案
相关题目
 是定义在
是定义在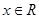 上以2为周期的偶函数,已知
上以2为周期的偶函数,已知 ,
,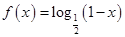 ,则函数
,则函数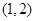 上( )
上( )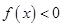
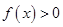
 ,若
,若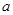 是从
是从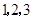 三个数中任取的一个数,
三个数中任取的一个数, 是从
是从 三个数中任取的一个数,则该函数有两个极值点的概率为( )
三个数中任取的一个数,则该函数有两个极值点的概率为( )

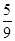

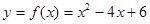 ,
,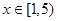 的值域.
的值域.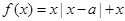 在R上为单调函数,则a的取值范围是 .
在R上为单调函数,则a的取值范围是 .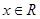 ,奇函数
,奇函数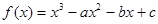 在
在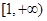 上单调,则实数b的取值范围是__________.
上单调,则实数b的取值范围是__________.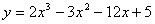 在
在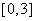 上的最小值是
上的最小值是 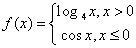 的图象上关于原点
的图象上关于原点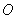 对称的点有 对.
对称的点有 对. 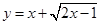 的值域是( )
的值域是( )