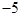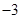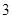题目内容
设 是定义在
是定义在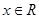 上以2为周期的偶函数,已知
上以2为周期的偶函数,已知 ,
,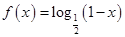 ,则函数
,则函数 在
在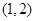 上( )
上( )
 是定义在
是定义在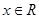 上以2为周期的偶函数,已知
上以2为周期的偶函数,已知 ,
,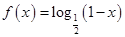 ,则函数
,则函数 在
在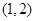 上( )
上( )A.是增函数且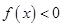 | B.是增函数且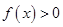 |
C.是减函数且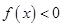 | D.是减函数且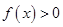 |
D
试题分析:设 x∈(-1,0),则-x∈(0,1),故 f(-x)=
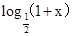 .
.又f(x)是定义在R上以2为周期的偶函数,故 f(x)=
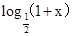 .
.再令 1<x<2,则-1<x-2<0,∴f(x-2)=
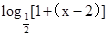 ,∴f(x)=
,∴f(x)=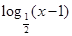 ,
,由1<x<2 可得 0<x-1<1,
故函数f(x)在(1,2)上是减函数,且f(x)>0,
故选D.
点评:典型题,利用奇偶性求函数的解析式,是常用处理方法,求出函数f(x)在(1,2)上 的解析式,是解题的关键。

练习册系列答案
相关题目
 ,满足
,满足 >
> ,则
,则 与
与 的大小关系是( )
的大小关系是( )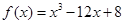 在区间
在区间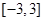 上的最大值与最小值分别为
上的最大值与最小值分别为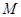 、
、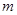 ,则
,则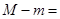 .
.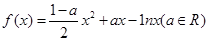 。
。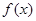 的极值;
的极值;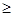 2时,讨论函数
2时,讨论函数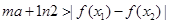 成立,求
成立,求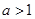 ,若函数
,若函数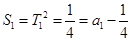 在区间
在区间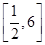 上是增函数,则
上是增函数,则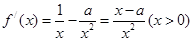 的取值范围是 .
的取值范围是 .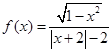 (2)
(2)
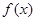 的定义域为
的定义域为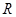 ,若存在常数
,若存在常数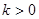 ,使
,使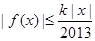 对一切实数
对一切实数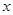 均成立
均成立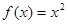 ;②
;②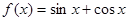 ;③
;③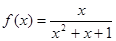 ;④
;④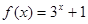 .
.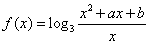 ,
,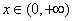 ,是否存在实数
,是否存在实数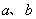 ,使
,使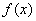 同时满足下列两个条件:(1)
同时满足下列两个条件:(1)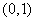 上是减函数,在
上是减函数,在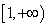 上是增函数;(2)
上是增函数;(2)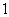 ,若存在,求出
,若存在,求出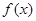 是连续的偶函数,且当
是连续的偶函数,且当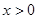 时,
时,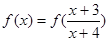 的所有
的所有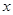 之和为( )
之和为( )