题目内容
【题目】《九章算木》中将底面为长方形，且有一条侧棱与底面垂直的四棱锥称之为“阳马”，现有一阳马，其正视图和侧视图是如图所示的直角三角形，该“阳马”的体积为
，若该阳马的顶点都在同一个球面上，则该球的表面积为（ ）
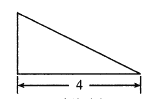
正视图 侧视图
A. 
B. 
C. 
D. 
【答案】D
【解析】
该几何体为四棱锥P﹣ABCD,底面ABCD为矩形，其中PD⊥底面ABCD．因为“阳马”的体积为
，所以利用V
= ，得PD=2, 则该阳马的外接球的直径利用勾股定理可以求出，即可求出球的表面积.
如图所示，该几何体为四棱锥P﹣ABCD．底面ABCD为矩形，
其中PD⊥底面ABCD．AB=2，AD=4，因为“阳马”的体积为，
所以V =
所以PD=2．
则该阳马的外接球的直径为PB=
．所以r=
∴该阳马的外接球的体积
．
故选：D．
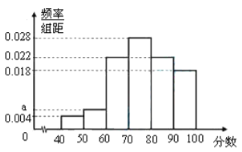
【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题．该企业为了检查生产该产品的甲，乙两条流水线的生产情况，随机地从这两条流水线上生产的大量产品中各抽取50件产品作为样本，测出它们的这一项质量指标值．若该项质量指标值落在
内，则为合格品，否则为不合格品．表1是甲流水线样本的频数分布表，图1是乙流水线样本的频率分布直方图．
（Ⅰ）根据图１，估计乙流水线生产产品该质量指标值的中位数；
（Ⅱ）若将频率视为概率，某个月内甲，乙两条流水线均生产了5000件产品，则甲，乙两条流水线分别生产出不合格品约多少件？
（Ⅲ）根据已知条件完成下面
列联表，并回答是否有85%的把握认为“该企业生产的这种产品的质量指标值与甲，乙两条流水线的选择有关”？
甲生产线 | 乙生产线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附：
（其中
为样本容量）
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
【题目】今年年初，中共中央、国务院发布《关于开展扫黑除恶专项斗争的通知》，在全国范围部署开展扫黑除恶专项斗争.那么这次的“扫黑除恶”专项斗争与2000年、2006年两次在全国范围内持续开展了十多年的“打黑除恶”专项斗争是否相同呢？某高校一个社团在年后开学后随机调查了
位该校在读大学生，就“扫黑除恶”与“打黑除恶”是否相同进行了一次调查，得到具体数据如表：
不相同 | 相同 | 合计 | |
男 |
|
|
|
女 |
|
|
|
合计 |
|
|
|
（1）根据如上的
列联表，能否在犯错误的概率不超过
的前提下，认为“扫黑除恶”与“打黑除恶”是否相同与性别有关"？
（2）计算这位大学生认为“扫黑除恶”与“打黑除恶”不相同的频率，并据此估算该校
名在读大学生中认为“扫黑除恶”与“打黑除恶”不相同的人数；
（3）为了解该校大学生对“扫黑除恶”与“打黑除恶”不同之处的知道情况，该校学生会组织部选取
位男生和
位女生逐个进行采访，最后再随机选取次采访记录放到该大学的官方网站上，求最后被选取的次采访对象中至少有一位男生的概率.
参考公式：
.
附表：
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
