题目内容
【题目】选修4﹣5:不等式选讲
已知函数f(x)=|x+1|﹣|x|+a.
(1)若a=0,求不等式f(x)≥0的解集;
(2)若方程f(x)=x有三个不同的解,求a的取值范围.
【答案】
(1)解:若a=0,f(x)=|x+1|﹣|x|= 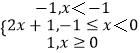 ,
,
∴当 x<﹣1时,不等式 即﹣1≥0,解得x∈.
当﹣1≤x<0时,不等式即 2x+1≥0,解得 x≥﹣ ![]() .综合可得﹣
.综合可得﹣ ![]() ≤x<0.
≤x<0.
当x≥0 时,不等式即 1≥0,恒成立,故不等式的解集为x≥0.
综上,不等式的解集为[﹣ ![]() ,+∞).
,+∞).
(2)解:设u(x)=|x+1|﹣|x|,则函数u(x)的图象和 y=x的图象如下图:
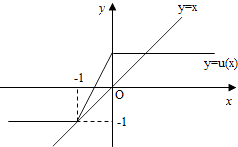
由题意易知,把函数y=u(x)的图象向下平移1个单位以内(不包括1个单位)与y=x的图象始终有3个交点,
从而﹣1<a<0.
【解析】(1)若a=0,则f(x)= 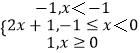 ,分 x<﹣1时、当﹣1≤x<0时、当x≥0 时,三种情况,分别求得不等式的解集,再取并集,即得所求.(2)设u(x)=|x+1|﹣|x|,由题意易知,把函数y=u(x)的图象向下平移1个单位以内(不包括1个单位)与y=x的图象始终有3个交点,从而求得a的范围.
,分 x<﹣1时、当﹣1≤x<0时、当x≥0 时,三种情况,分别求得不等式的解集,再取并集,即得所求.(2)设u(x)=|x+1|﹣|x|,由题意易知,把函数y=u(x)的图象向下平移1个单位以内(不包括1个单位)与y=x的图象始终有3个交点,从而求得a的范围.
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.

练习册系列答案
相关题目