题目内容
【题目】经市场调查,某种商品在过去50天的销量和价格均为销售时间t(天)的函数,且销售量近似地满足f(t)=-2t+200(1≤t≤50,t∈N),前30天价格为g(t)=![]() t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).
t+30(1≤t≤30,t∈N),后20天价格为g(t)=45(31≤t≤50,t∈N).
(1)写出该种商品的日销售额S与时间t的函数关系式;
(2)求日销售额S的最大值.
【答案】(1)S=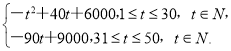 (2)6400.
(2)6400.
【解析】(1)根据题意得
S=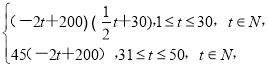
即S=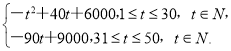
(2)①当1≤t≤30,t∈N时,S=-(t-20)2+6400,
当t=20时,S的最大值为6400;
②当31≤t≤50,t∈N时,S=-90t+9000为减函数,
当t=31时,S的最大值是6210,
∵6210<6400,∴当t=20时,日销售额S有最大值6400.

练习册系列答案
相关题目
【题目】一台机器按不同的转速生产出来的某机械零件有一些会有缺点,每小时生产有缺点的零件的多少随机器的运转的速度的变化而变化,下表为抽样试验的结果:
转速 | 16 | 14 | 12 | 8 |
每小时生产有缺点的零件数 | 11 | 9 | 8 | 5 |
(1)画出散点图;
(2)如果![]() 对
对![]() 有线性相关关系,请画出一条直线近似地表示这种线性关系;
有线性相关关系,请画出一条直线近似地表示这种线性关系;
(3)在实际生产中,若它们的近似方程为![]() ,允许每小时生产的产品中有缺点的零件最多为
,允许每小时生产的产品中有缺点的零件最多为![]() 件,那么机器的运转速度应控制在什么范围内?
件,那么机器的运转速度应控制在什么范围内?