题目内容
【题目】已知等差数列![]() 的前
的前![]() 项和为
项和为![]() ,等比数列
,等比数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,![]() ,
,![]() .
.
(1)若![]() ,求
,求![]() 的通项公式;
的通项公式;
(2)若![]() ,求
,求![]() .
.
【答案】(1)![]() ;(2)21或
;(2)21或![]() .
.
【解析】试题分析:(1)设等差数列![]() 公差为
公差为![]() ,等比数列
,等比数列![]() 公比为
公比为![]() ,由已知条件求出
,由已知条件求出![]() ,再写出通项公式;(2)由
,再写出通项公式;(2)由![]() ,求出
,求出![]() 的值,再求出
的值,再求出![]() 的值,求出
的值,求出![]() 。
。
试题解析:设等差数列![]() 公差为
公差为![]() ,等比数列
,等比数列![]() 公比为
公比为![]() 有
有![]() ,即
,即![]() .
.
(1)∵![]() ,结合
,结合![]() 得
得![]() ,
,
∴![]() .
.
(2)∵![]() ,解得
,解得![]() 或3,
或3,
当![]() 时,
时,![]() ,此时
,此时![]() ;
;
当![]() 时,
时,![]() ,此时
,此时![]() .
.
【题型】解答题
【结束】
20
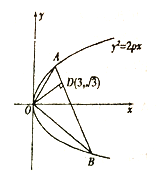
【题目】如图,已知直线与抛物线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,
, ![]() 交
交![]() 于
于![]() ,且点
,且点![]() 的坐标为
的坐标为![]() .
.
(1)求![]() 的值;
的值;
(2)若![]() 为抛物线的焦点,
为抛物线的焦点, ![]() 为抛物线上任一点,求
为抛物线上任一点,求![]() 的最小值.
的最小值.
【答案】(1)![]() .(2)4.
.(2)4.
【解析】试题分析:(1)设A(x1,y1),B(x2,y2),由AB⊥OD,kOD=![]() ,可得直线AB的斜率k=-
,可得直线AB的斜率k=-![]() ,得到直线AB的方程为
,得到直线AB的方程为![]() ,与抛物线方程联立化为
,与抛物线方程联立化为![]() ∴
∴![]() ,由
,由![]() 得
得![]() ,即
,即![]() ,∴
,∴![]() ,即可解得
,即可解得![]() 的值;
的值;
(2)过点M作直线的垂线MN,垂足为N,则|MF|=|MN|,由抛物线定义知![]() 的最小值为
的最小值为![]() 点到抛物线
点到抛物线![]() 准线的距离.
准线的距离.
试题解析:
(1)设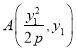 ,
, 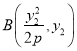 ,
, ![]() ,
,
则![]() ,直线
,直线![]() 的方程为
的方程为![]() ,
,
即![]() .将
.将![]() 代入上式,
代入上式,
整理得![]() ,∴
,∴![]() ,由
,由![]() 得
得![]() ,即
,即
![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴![]() .
.
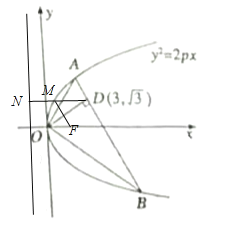
(2)过点M作直线的垂线MN,垂足为N,则|MF|=|MN|,由抛物线定义知![]() 的最小值为
的最小值为![]() 点到抛物线
点到抛物线![]() 准线的距离,又准线方程为
准线的距离,又准线方程为![]() ,因此
,因此![]() 的最小值为DN=4.
的最小值为DN=4.

【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对![]() 名小学六年级学生进行了问卷调查,并得到如下列联表.平均每天喝
名小学六年级学生进行了问卷调查,并得到如下列联表.平均每天喝![]() 以上为“常喝”,体重超过
以上为“常喝”,体重超过![]() 为“肥胖”.
为“肥胖”.
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
合计 | 30 |
已知在全部![]() 人中随机抽取
人中随机抽取![]() 人,抽到肥胖的学生的概率为
人,抽到肥胖的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有![]() 的把握认为肥胖与常喝碳酸饮料有关?请说明你的理由;
的把握认为肥胖与常喝碳酸饮料有关?请说明你的理由;
(3)已知常喝碳酸饮料且肥胖的学生中恰有2名女生,现从常喝碳酸饮料且肥胖的学生中随机抽取2人参加一个有关健康饮食的电视节目,求恰好抽到一名男生和一名女生的概率.
附:![]()
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|

