题目内容
【题目】已知数列{an}的前n项和为Sn , Sn=n2+n.
(Ⅰ)求{an}的通项公式an;
(Ⅱ)若ak+1 , a2k , a2k+3(k∈N*)恰好依次为等比数列{bn}的第一、第二、第三项,求数列{ ![]() }的前n项和Tn .
}的前n项和Tn .
【答案】解:(Ⅰ)当n=1时,a1=S1=2.当n≥2时,an=Sn﹣Sn﹣1=(n2+n)﹣[(n﹣1)2+(n﹣1)]=2n.
检验n=1时,上式符合.
∴an=2n..
(Ⅱ)由题知:ak+1 , a2k , a2k+3(k∈N*)恰好依次为等比数列{bn}的第一、第二、第三项,
∴ ![]() =ak+1a2k+3(k∈N*),
=ak+1a2k+3(k∈N*),
即(2×2k)2=2(k+1)2(2k+3),解得k=3.
∴b1=a4=8,b2=a6=12,公比q= ![]() =
= ![]() .
.
∴bn= ![]() ,
,
∴ ![]() =
= ![]() ,
,
∴Tn= ![]()
![]() +
+ ![]() +…+
+…+ 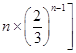 .
.![]() =
= 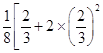 +…+
+…+ 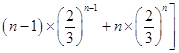 ,
,
∴ ![]() =
= 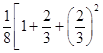 +…+
+…+ 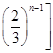 ﹣
﹣ ![]() =
= ![]() ﹣
﹣ ![]() ×
× ![]() ,
,
Tn= ![]() ﹣
﹣ ![]() ×
× ![]() .
.
【解析】(Ⅰ)当n=1时,a1=S1=2.当n≥2时,an=Sn﹣Sn﹣1 , 即可得出.(Ⅱ)由题知:ak+1 , a2k , a2k+3(k∈N*)恰好依次为等比数列{bn}的第一、第二、第三项,可得 ![]() =ak+1a2k+3(k∈N*),解得k=3.可得bn=
=ak+1a2k+3(k∈N*),解得k=3.可得bn= ![]() ,
, ![]() =
= ![]() ,再利用“错位相减法”与求和公式即可得出.
,再利用“错位相减法”与求和公式即可得出.
【考点精析】掌握数列的前n项和是解答本题的根本,需要知道数列{an}的前n项和sn与通项an的关系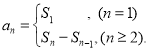 .
.

【题目】2018年6月19日凌晨某公司公布的年中促销全天交易数据显示,天猫年中促销当天全天下单金额为1592亿元.为了了解网购者一次性购物情况,某统计部门随机抽查了6月18日100名网购者的网购情况,得到如下数据统计表,已知网购金额在2000元以上(不含2000元)的频率为0.4.

网购金额(元) | 频数 | 频率 |
| 5 | 0.05 |
|
|
|
| 15 | 0.15 |
| 25 | 0.25 |
| 30 | 0.3 |
|
|
|
合计 | 100 | 1 |
(Ⅰ)先求出![]() 的值,再将图中所示的频率分布直方图绘制完整;
的值,再将图中所示的频率分布直方图绘制完整;
(Ⅱ)对这100名网购者进一步调查显示:购物金额在2000元以上的购物者中网龄3年以上的有35人,购物金额在2000元以下(含2000元)的购物者中网龄不足3年的有20人,请填写下面的列联表,并据此判断能否在犯错误的概率不超过0.025的前提下认为网购金额超过2000元与网龄在3年以上有关?
网龄3年以上 | 网龄不足3年 | 总计 | |
购物金额在2000元以上 | 35 | ||
购物金额在2000元以下 | 20 | ||
总计 | 100 |
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
参考公式:![]() 其中
其中![]() .
.
(Ⅲ)从这100名网购者中根据购物金额分层抽出20人给予返券奖励,为进一步激发购物热情,在![]() 和
和![]() 两组所抽中的8人中再随机抽取2人各奖励1000元现金,求
两组所抽中的8人中再随机抽取2人各奖励1000元现金,求![]() 组获得现金奖的数学期望.
组获得现金奖的数学期望.
