��Ŀ����
����Ŀ��2018��6��19���賿ij��˾���������д���ȫ�콻��������ʾ����è���д�������ȫ���µ����Ϊ1592��Ԫ.Ϊ���˽�������һ���Թ��������ijͳ�Ʋ�����������6��18��100�������ߵ�����������õ���������ͳ�Ʊ�����֪���������2000Ԫ����(����2000Ԫ)��Ƶ��Ϊ0.4.

�������(Ԫ) | Ƶ�� | Ƶ�� |
| 5 | 0.05 |
|
|
|
| 15 | 0.15 |
| 25 | 0.25 |
| 30 | 0.3 |
|
|
|
�ϼ� | 100 | 1 |
(��)�����![]() ��ֵ���ٽ�ͼ����ʾ��Ƶ�ʷֲ�ֱ��ͼ����������
��ֵ���ٽ�ͼ����ʾ��Ƶ�ʷֲ�ֱ��ͼ����������
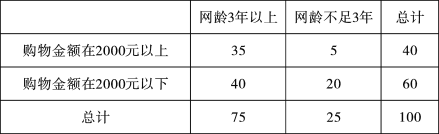
(��)����100�������߽�һ��������ʾ����������2000Ԫ���ϵĹ�����������3�����ϵ���35�ˣ���������2000Ԫ����(��2000Ԫ)�Ĺ����������䲻��3�����20�ˣ�����д����������������ݴ��ж��ܷ��ڷ�����ĸ��ʲ�����0.025��ǰ������Ϊ��������2000Ԫ��������3�������йأ�
����3������ | ���䲻��3�� | �ܼ� | |
��������2000Ԫ���� | 35 | ||
��������2000Ԫ���� | 20 | ||
�ܼ� | 100 |
�ο����ݣ�
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.076 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
�ο���ʽ��![]() ����
����![]() .
.
������100���������и��ݹ�����ֲ���20�˸��践ȯ������Ϊ��һ�������������飬��![]() ��
��![]() ���������е�8�����������ȡ2�˸�����1000Ԫ�ֽ���
���������е�8�����������ȡ2�˸�����1000Ԫ�ֽ���![]() �����ֽ���ѧ����.
�����ֽ���ѧ����.
���𰸡�(��)������; (��)�ڷ�����ĸ��ʲ�����0.025��ǰ������Ϊ��������2000Ԫ��������3�������й�������1500.
��������
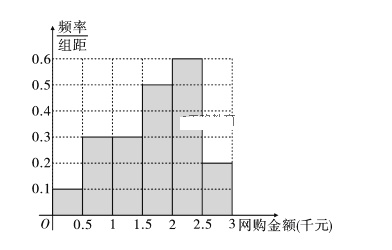
(��)�������֪2000Ԫ���ϣ�����2000Ԫ����Ƶ��Ϊ0.4���������������(2500��3000]��Ƶ��Ϊ0.40.3=0.1���ɴ��ٽ��Ƶ�ʷֲ�ֱ��ͼ��Ƶ�ʷֲ����ɷֱ����![]() ��ֵ���������ݲ�ȫƵ�ʷֲ�ֱ��ͼ��(��)�Ȳ�ȫ2��2���������ɱ����������K2
��ֵ���������ݲ�ȫƵ�ʷֲ�ֱ��ͼ��(��)�Ȳ�ȫ2��2���������ɱ����������K2![]() ��������(2000��2500]�������XΪ0��1��2����ø��ʼ�������
��������(2000��2500]�������XΪ0��1��2����ø��ʼ�������
������Ϊ���������2000Ԫ���ϣ�����2000Ԫ����Ƶ��Ϊ0.4��
�������������(2500��3000]��Ƶ��Ϊ0.40.3=0.1��
��q=0.1����y=100��0.1=10��
�Ӷ�x=15��p=0.15����Ӧ��Ƶ�ʷֲ�ֱ��ͼ��ͼ2��ʾ��
������Ӧ��2��2������Ϊ��
�ɹ�ʽK2=![]() ��
��
��Ϊ5.56>5.024��
���Ծݴ��������жϣ��ڷ�����ĸ��ʲ�����0.025��ǰ������Ϊ��������2000Ԫ��������3�������йأ�
������(2000��2500]��(2500��3000]�����������8�����ٳ�ȡ2�˸�����1000Ԫ�ֽ���(2000��2500]�������XΪ0��1��2��
��![]()
![]() ��
��
��(2000��2500]�����ֽ���ѧ����![]() +1000
+1000![]() +2000
+2000![]() =1500��
=1500��

 ��ĩ1�����ʽ���������ϵ�д�
��ĩ1�����ʽ���������ϵ�д�����Ŀ��![]() ��ָ������ֱ��С�ڻ����
��ָ������ֱ��С�ڻ����![]() �Ŀ����Ҳ�ƿ���ο����.Ϊ��̽����������
�Ŀ����Ҳ�ƿ���ο����.Ϊ��̽����������![]() ��Ũ���Ƿ���أ��ֲɼ���ij������һ������ijһʱ��γ�������
��Ũ���Ƿ���أ��ֲɼ���ij������һ������ijһʱ��γ�������![]() ���������±���
���������±���
ʱ�� | ��һ | �ܶ� | ���� | ���� | ���� |
������ |
|
|
|
|
|
|
|
|
|
|
|
�������ϱ����ݣ���������������ϵ�л���ɢ��ͼ��
�������ϱ����ݣ�����С���˷����![]() ����
����![]() �����Իع鷽��
�����Իع鷽��![]() ��
��
����������ͬһʱ��εij�������![]() �������Ը��ݣ�����������Իع鷽�̣�Ԥ���ʱ
�������Ը��ݣ�����������Իع鷽�̣�Ԥ���ʱ![]() ��Ũ��Ϊ���٣�������������
��Ũ��Ϊ���٣�������������
�ο���ʽ������С���˷����ûع�ֱ�ߵķ����ǣ�![]() ��
��
���� ��
��