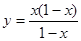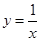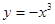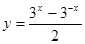题目内容
设f(x)是连续的偶函数,且当x>0时是单调函数,则满足f(x)=f(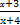
)的所有x之和为( )
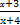)的所有x之和为( )| A．-3 | B．3 | C．-8 | D．8 |
C
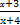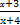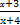因为f(x)是连续的偶函数,且x>0时是单调函数,由偶函数的性质可知若f(x)=f(),只有两种情况:①x=;②x+=0,
由①知x2+3x-3=0,故两根之和为x1+x2=-3,
由②知x2+5x+3=0,故其两根之和为x3+x4=-5.
因此满足条件的所有x之和为-8.
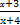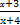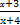),只有两种情况:①x=;②x+=0,由①知x2+3x-3=0,故两根之和为x1+x2=-3,
由②知x2+5x+3=0,故其两根之和为x3+x4=-5.
因此满足条件的所有x之和为-8.
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
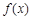是定义在R上的偶函数, 且在区间
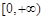单调递增．若实数
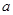满足
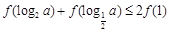,则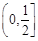
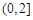
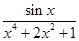的最大值与最小值的和为 .
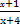)的所有x之和为( )
]恒成立,则a的最小值是( )
