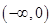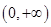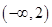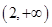题目内容
若不等式x2+ax+1≥0对于一切x∈(0, ]恒成立,则a的最小值是( )
]恒成立,则a的最小值是( )
 ]恒成立,则a的最小值是( )
]恒成立,则a的最小值是( )| A.0 | B.2 | C.- | D.-3 |
C
方法一:设g(a)=ax+x2+1,
∵x∈(0, ],∴g(a)为单调递增函数.
],∴g(a)为单调递增函数.
当x= 时满足:
时满足: a+
a+ +1≥0即可,解得a≥-
+1≥0即可,解得a≥- .
.
方法二:由x2+ax+1≥0得a≥-(x+ )在x∈(0,
)在x∈(0, ]上恒成立,
]上恒成立,
令g(x)=-(x+ ),则知g(x)在(0,
),则知g(x)在(0, ]为增函数,
]为增函数,
∴g(x)max=g( )=-
)=- ,∴a≥-
,∴a≥- .
.
∵x∈(0,
 ],∴g(a)为单调递增函数.
],∴g(a)为单调递增函数.当x=
 时满足:
时满足: a+
a+ +1≥0即可,解得a≥-
+1≥0即可,解得a≥- .
.方法二:由x2+ax+1≥0得a≥-(x+
 )在x∈(0,
)在x∈(0, ]上恒成立,
]上恒成立,令g(x)=-(x+
 ),则知g(x)在(0,
),则知g(x)在(0, ]为增函数,
]为增函数,∴g(x)max=g(
 )=-
)=- ,∴a≥-
,∴a≥- .
.
练习册系列答案
相关题目
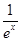 在区间(0,+∞)上的单调性.
在区间(0,+∞)上的单调性. ,若f(x)在(0,+∞)上单调递增,则实数a的取值范围为________.
,若f(x)在(0,+∞)上单调递增,则实数a的取值范围为________.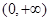 上单调递增的是( )
上单调递增的是( )
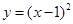
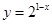
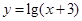
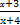 )的所有x之和为( )
)的所有x之和为( ) ),f(-1)的大小关系为( )
),f(-1)的大小关系为( )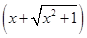 ,则不等式f(m)+f(m2-2)≥0(m∈R)成立的充要条件是________.(注:填写m的取值范围)
,则不等式f(m)+f(m2-2)≥0(m∈R)成立的充要条件是________.(注:填写m的取值范围)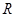 上的可导函数
上的可导函数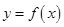 的导函数为
的导函数为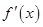 ,满足
,满足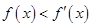 ,且
,且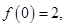 则不等式
则不等式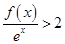 的解集为( )
的解集为( )