题目内容
已知函数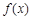 是定义在R上的偶函数, 且在区间
是定义在R上的偶函数, 且在区间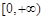 单调递增.若实数
单调递增.若实数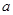 满足
满足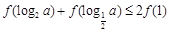 ,则
,则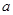 的取值范围是( )
的取值范围是( )
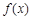 是定义在R上的偶函数, 且在区间
是定义在R上的偶函数, 且在区间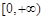 单调递增.若实数
单调递增.若实数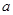 满足
满足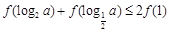 ,则
,则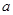 的取值范围是( )
的取值范围是( )A.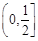 | B.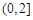 | C. | D. |
D
试题分析:根据偶函数性质:
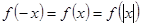 ,
, ,
,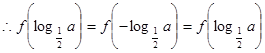 ,所以原式等价于
,所以原式等价于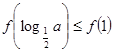 ,根据
,根据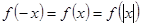 ,即
,即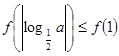 ,在区间
,在区间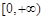 单调递增,所以
单调递增,所以 解得
解得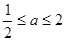 ,故选D.
,故选D.
练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
题目内容
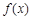 是定义在R上的偶函数, 且在区间
是定义在R上的偶函数, 且在区间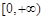 单调递增.若实数
单调递增.若实数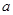 满足
满足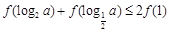 ,则
,则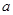 的取值范围是( )
的取值范围是( )A.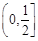 | B.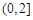 | C. | D. |
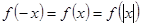 ,
, ,
,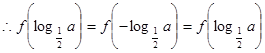 ,所以原式等价于
,所以原式等价于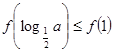 ,根据
,根据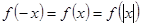 ,即
,即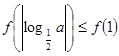 ,在区间
,在区间 单调递增,所以
单调递增,所以 解得
解得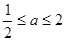 ,故选D.
,故选D.
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案