题目内容
3.抛物线y2=4x的焦点为F,点P为抛物线上的动点,若A(-1,0),则$\frac{{|{PF}|}}{{|{PA}|}}$的最小值为$\frac{\sqrt{2}}{2}$.分析 过点P作PM垂直于准线,M为垂足,则由抛物线的定义可得|PF|=|PM|,则$\frac{{|{PF}|}}{{|{PA}|}}$=$\frac{|PM|}{|PA|}$=sin∠PAM,故当PA和抛物线相切时,$\frac{{|{PF}|}}{{|{PA}|}}$最小.再利用直线的斜率公式、导数的几何意义求得切点的坐标,从而求得$\frac{{|{PF}|}}{{|{PA}|}}$的最小值.
解答  解:由题意可得,焦点F(1,0),准线方程为x=-1.
解:由题意可得,焦点F(1,0),准线方程为x=-1.
过点P作PM垂直于准线,M为垂足,
则由抛物线的定义可得|PF|=|PM|,
则$\frac{{|{PF}|}}{{|{PA}|}}$=$\frac{|PM|}{|PA|}$=sin∠PAM,∠PAM 为锐角.
故当∠PAM 最小时,$\frac{{|{PF}|}}{{|{PA}|}}$最小,
故当PA和抛物线相切时,$\frac{{|{PF}|}}{{|{PA}|}}$最小.
设切点P(a,2$\sqrt{a}$),则PA的斜率为$\frac{2\sqrt{a}-0}{a+1}$=(2$\sqrt{x}$)′=$\frac{1}{\sqrt{a}}$,
求得a=1,可得P(1,2),∴|PM|=2|PA|=2$\sqrt{2}$,
∴sin∠PAM=$\frac{|PM|}{|PA|}$=$\frac{2}{2\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题主要考查抛物线的定义、性质的简单应用,直线的斜率公式、导数的几何意义,属于中档题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
16.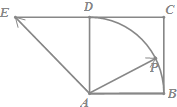 如图,四边形ABCD是正方形,延长CD至E,使DE=CD,若点P是以点A为圆心,AB为半径的圆弧(不超出正方形)上的任一点,设向量$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ的最小值为( )
如图,四边形ABCD是正方形,延长CD至E,使DE=CD,若点P是以点A为圆心,AB为半径的圆弧(不超出正方形)上的任一点,设向量$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ的最小值为( )
 如图,四边形ABCD是正方形,延长CD至E,使DE=CD,若点P是以点A为圆心,AB为半径的圆弧(不超出正方形)上的任一点,设向量$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ的最小值为( )
如图,四边形ABCD是正方形,延长CD至E,使DE=CD,若点P是以点A为圆心,AB为半径的圆弧(不超出正方形)上的任一点,设向量$\overrightarrow{AP}=λ\overrightarrow{AB}+μ\overrightarrow{AE}$,则λ+μ的最小值为( )| A. | $\sqrt{5}$ | B. | 1 | C. | $\sqrt{2}$ | D. | 2 |
18.阅读如图所示的程序框图,若输出的数据为58,则判断框中应填入的条件为( )


| A. | k≤3 | B. | k≤4 | C. | k≤5 | D. | k≤6 |
15.定义在区间[a,b](b>a)上的函数$f(x)=\frac{1}{2}sinx-\frac{{\sqrt{3}}}{2}cosx$的值域是$[-\frac{1}{2},1]$,则b-a的最大值M和最小值m分别是( )
| A. | $m=\frac{π}{6},M=\frac{π}{3}$ | B. | $m=\frac{π}{3},M=\frac{2π}{3}$ | C. | $m=\frac{4π}{3},M=2π$ | D. | $m=\frac{2π}{3},M=\frac{4π}{3}$ |
12.已知i为虚数单位,复数z满足1+i+(1+i)2z=(1-i)2,则复数z的虚部为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{2}i$ | C. | $\frac{3}{2}$ | D. | $-\frac{3}{2}$ |
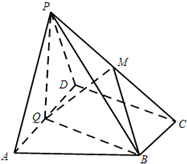 如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,$BC=\frac{1}{2}AD=1$,$CD=\sqrt{3}$.
如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,AD∥BC,∠ADC=90°,平面PAD⊥底面ABCD,Q为AD的中点,M是棱PC上的点,PA=PD=2,$BC=\frac{1}{2}AD=1$,$CD=\sqrt{3}$.