题目内容
【题目】设p：A={x|2x2﹣3ax+a2＜0}，q：B={x|x2+3x﹣10≤0}．
（1）求A；
（2）当a＜0时，若￢p是￢q的必要不充分条件，求a的取值范围．
【答案】
（1）解：关于p：A={x|2x2﹣3ax+a2＜0}，
解不等式2x2﹣3ax+a2＜0，得：
a＞0时： 
＜x＜a；a＜0时：a＜x＜ ，
∴a＞0时：A=[ ，a]；a＜0时：A=[a， ]；
（2）解：当a＜0时：A=[a， ]，B=[﹣5，2]，
若￢p是￢q的必要不充分条件，
则q是p的必要不充分条件，
即AB，
∴ 
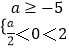，解得：﹣5≤a＜0
【解析】（1）通过讨论a的范围，解不等式求出集合A即可；（2）先求出集合A，B，问题转化为A是B的子集，得到关于a的不等式组，解出即可．
练习册系列答案
名校课堂系列答案
相关题目
