Question

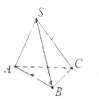
【题目】如图，在四棱锥P-ABCD中，AD∥BC，ADC=PAB=90°，BC=CD=AD.E为棱AD的中点，异面直线PA与CD所成的角为90°.

（I）在平面PAB内找一点M，使得直线CM∥平面PBE，并说明理由；

(II)若二面角P-CD-A的大小为45°，求直线PA与平面PCE所成角的正弦值.

Answer 1

【答案】（Ⅰ）见解析；（Ⅱ） .

【解析】试题分析：本题考查线面平行、线线平行、向量法等基础知识，考查空间想象能力、分析问题的能力、计算能力.第一问，利用线面平行的定理，先证明线线平行，再证明线面平行；第二问，可以先找到线面角，再在三角形中解出正弦值，还可以用向量法建立直角坐标系解出正弦值.

试题解析：（Ⅰ）在梯形ABCD中，AB与CD不平行.

延长AB，DC，相交于点M（M∈平面PAB），点M即为所求的一个点.理由如下：

由已知，BC∥ED，且BC=ED.

所以四边形BCDE是平行四边形.

从而CM∥EB.

又EB平面PBE，CM平面PBE，

所以CM∥平面PBE.

（说明：延长AP至点N，使得AP=PN，则所找的点可以是直线MN上任意一点）

（Ⅱ）方法一：

由已知，CD⊥PA，CD⊥AD，PAAD=A，

所以CD⊥平面PAD.

从而CD⊥PD.

所以PDA是二面角P-CD-A的平面角.

所以PDA=45°.

设BC=1，则在Rt△PAD中，PA=AD=2.

过点A作AH⊥CE，交CE的延长线于点H，连接PH.

易知PA⊥平面ABCD，

从而PA⊥CE.

于是CE⊥平面PAH.

所以平面PCE⊥平面PAH.

过A作AQ⊥PH于Q，则AQ⊥平面PCE.

所以APH是PA与平面PCE所成的角.

在Rt△AEH中，AEH=45°，AE=1，

所以AH=.

在Rt△PAH中，PH==，

所以sinAPH==.

方法二：

由已知，CD⊥PA，CD⊥AD，PAAD=A，

所以CD⊥平面PAD.

于是CD⊥PD.

从而PDA是二面角P-CD-A的平面角.

所以PDA=45°.

由PA⊥AB，可得PA⊥平面ABCD.

设BC=1，则在Rt△PAD中，PA=AD=2.

作Ay⊥AD，以A为原点，以,的方向分别为x轴，z轴的正方向，建立如图所示的空间直角坐标系A-xyz，则A（0,0,0），P（0,0,2），C(2,1,0)，E(1,0,0)，

所以=（1,0,-2），=（1,1,0），=（0,0,2）

设平面PCE的法向量为n=(x,y,z)，

由得设x=2，解得n=(2,-2,1).

设直线PA与平面PCE所成角为α，则sinα==.

所以直线PA与平面PCE所成角的正弦值为.