Question

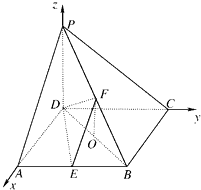
【题目】如图，在四棱锥P﹣ABCD中，PD⊥底面ABCD，底面ABCD为正方形，PD=DC，E、F分别是AB、PB的中点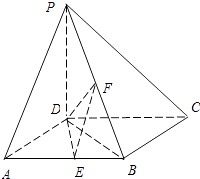

（1）求证：EF⊥CD；
（2）在平面PAD内求一点G，使GF⊥平面PCB，并证明你的结论；
（3）求DB与平面DEF所成角的正弦值．

Answer 1

【答案】
（1）证明：以DA、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系（如图），

设AD=a，则D（0，0，0）、A（a，0，0）、B（a，a，0）、C（0，a，0）、E（a， ，0）、F（ ， ， ）、P（0，0，a）

∵ =（﹣ ，0， ）， =（0，a，0），

∴ =（﹣ ，0， ）（0，a，0）=0，

∴ ⊥

∴EF⊥DC

（2）解：设G（x，0，z），则G∈平面PAD．

=（x﹣ ，﹣ ，z﹣ ），

=（x﹣ ，﹣ ，z﹣ ）（a，0，0）=a（x﹣ ）=0，∴x= ；

=（x﹣ ，﹣ ，z﹣ ）（0，﹣a，a）= +a（z﹣ ）=0，∴z=0．

∴G点坐标为（ ，0，0），即G点为AD的中点

（3）解：设平面DEF的法向量为 =（x，y，z）．

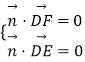由 得：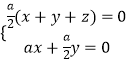

取x=1，则y=﹣2，z=1，

∴ =（1，﹣2，1）．

cos＜ ， ＞= = = ，

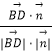∴DB与平面DEF所成角的正弦值的大小为

【解析】以DA、DC、DP所在直线为x轴、y轴、z轴建立空间直角坐标系，设AD=a，可求出各点的坐标；（1）求出EF和CD的方向向量，根据向量垂直的充要条件，可证得 ⊥ ，即EF⊥DC．（2）设G（x，0，z），根据线面垂直的性质，可得 = =0，进而可求出x，z值，得到G点的位置；（3）求出平面DEF的法向量为 ，及DB的方向 的坐标，代入向量夹角公式，可得DB与平面DEF所成角的正弦值
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识，掌握一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想，以及对直线与平面垂直的性质的理解，了解垂直于同一个平面的两条直线平行．