题目内容
【题目】已知函数![]()
(1)作出函数f(x)的大致图象;
(2)写出函数f(x)的单调区间;
(3)当![]() 时,由图象写出f(x)的最小值.
时,由图象写出f(x)的最小值.
【答案】(1); (2)增区间为![]() ,减区间为
,减区间为![]() ;(3)
;(3) .
.
【解析】
(1)化简函数的解析式为f(x)=![]() ,再利用二次函数的图象特征作出函数的图象;
,再利用二次函数的图象特征作出函数的图象;
(2)由(1)结合函数的图象可得函数f(x)的单调减区间以及单调增区间.
(3)分当![]() ≥1 和当0<
≥1 和当0<![]() <1两种情况,结合图象利用函数的单调性求出函数的最小值.
<1两种情况,结合图象利用函数的单调性求出函数的最小值.
(1)函数f(x)=|x|(x﹣a)=![]() ,如图所示:
,如图所示:
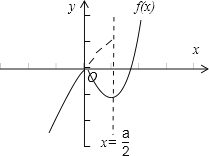
(2)由(1)可得函数f(x)的单调减区间为(0,![]() ),
),
单调增区间为(﹣∞,0),(![]() ,+∞).
,+∞).
(3)x>0时,f(x)=x2﹣ax,f(x)的图象的对称轴为x=![]() .
.
由a>0,可得当x∈[0,1]时,
若![]() ≥1,即a≥2时,fmin(x)=f(1)=1﹣a.
≥1,即a≥2时,fmin(x)=f(1)=1﹣a.
若0<![]() <1,即0<a<2时,fmin(x)=f(
<1,即0<a<2时,fmin(x)=f(![]() )=﹣
)=﹣![]() .
.
综上: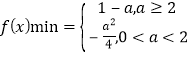

练习册系列答案
相关题目

