Question

【题目】已知函数为对数函数,并且它的图象经过点,函数=在区间上的最小值为,其中.

(1)求函数的解析式;

(2)求函数的最小值的表达式;

(3)是否存在实数同时满足以下条件:①;②当的定义域为时,值域为.若存在,求出的值;若不存在,说明理由.

Answer 1

【答案】（1）；（2）见解析；(3)m，n不存在

【解析】

（1）代入点的坐标，求出a的值，从而求出f（x）的解析式；

（2）设t=f（x）=log2x，通过讨论b的范围，求出函数的最小值即可；

（3）根据对数函数的性质求出m+n=8，得到矛盾，从而判断结论．

(1)设且)

∵的图象经过点,

∴,即,

∴,即,

∴.

(2)设==,

∵,

∴,

∴,即

则===,对称轴为

①当时,在上是增函数,

②当时,在上是减函数,在上是增函数,==

③当时,在上是减函数,

综上所述,=.

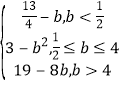(3),.

的定义域为,值域为,且为减函数,

，两式相减得,

,

得,但这与“”矛盾,

故满足条件的实数不存在.