题目内容
5.三个互不相等的实数成等差数列,适当交换这三个是的位置后,变成一个等比数列,则此等比数列的公比组成的集合为{$-\frac{1}{2}$,-2}.分析 据三个数构成等差数列设出三个数,通过讨论哪一个数是等比中项,分三种情况列出方程求出三个数,求出公比.
解答 解:设三个互不相等的实数为a-d,a,a+d,(d≠0)
交换这三个数的位置后:
①若a是等比中项,则a2=(a-d)(a+d),解得d=0,不符合;
②若a-d是等比中项,则(a-d)2=a(a+d),解得d=3a,
此时三个数为a,-2a,4a,公比为-2或三个数为4a,-2a,a,公比为$-\frac{1}{2}$,
③若a+d是等比中项,则同理得到公比为-2,或公比为$-\frac{1}{2}$
所以此等比数列的公比组成的集合是{$-\frac{1}{2}$,-2},
故答案为:{$-\frac{1}{2}$,-2}.
点评 本题考查三个数成等差数列的设法,等比中项的性质,以及分类讨论思想、方程思想的应用,属于中档题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
13.如图所示的程序框图,若输出的S是62,则①可以为( )
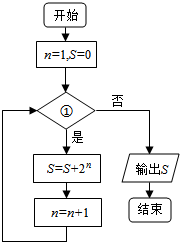

| A. | n≤3? | B. | n≤4? | C. | n≤5? | D. | n≤6? |
20.已知p:不等式|x+1|+|x-2|>m的解集为R;q:f(x)=log(5-2m)x为减函数,则p成立是q成立的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
14.假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:
若由资料知y对x呈线性相关关系.
(1)请画出上表数据的散点图;
(2)请根据最小二乘法求出线性回归方程$\widehat{y}$=bx+a的回归系数a,b;$b=\frac{\sum _{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum _{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}},a=\overline{y}-b\overline{x}$
(3)估计使用年限为10年时,维修费用是多少?
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)请画出上表数据的散点图;
(2)请根据最小二乘法求出线性回归方程$\widehat{y}$=bx+a的回归系数a,b;$b=\frac{\sum _{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum _{i=1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}},a=\overline{y}-b\overline{x}$
(3)估计使用年限为10年时,维修费用是多少?
15.如果椭圆的两焦点为F1(-1,0)和F2(1,0),P是椭圆上的一点,且|PF1|、|F1F2|、|PF2|成等差数列,那么椭圆的方程是( )
| A. | $\frac{x^2}{3}+\frac{y^2}{4}$=1 | B. | $\frac{x^2}{4}+\frac{y^2}{3}$=1 | C. | $\frac{x^2}{16}+\frac{y^2}{9}$=1 | D. | $\frac{x^2}{16}+\frac{y^2}{12}$=1 |