题目内容
4.设a>0,b>0,若1是a与b的等差中项,则$\frac{1}{a}$+$\frac{1}{b}$的最小值为( )| A. | 8 | B. | 4 | C. | 1 | D. | 2 |
分析 1是a与b的等差中项,可得a+b=2.再利用“乘1法”与基本不等式的性质即可得出.
解答 解:∵1是a与b的等差中项,
∴a+b=2.
则$\frac{1}{a}$+$\frac{1}{b}$=$\frac{1}{2}(a+b)$$(\frac{1}{a}+\frac{1}{b})$=$\frac{1}{2}(2+\frac{b}{a}+\frac{a}{b})$$≥\frac{1}{2}$$(2+2\sqrt{\frac{b}{a}•\frac{a}{b}})$=2,当且仅当a=b=1时取等号.
故选:D.
点评 本题考查了等差中项的性质、“乘1法”与基本不等式的性质,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
12.如图,在△OAB中,P为线段AB上的一点,若$\overrightarrow{{O}{P}}$=x$\overrightarrow{{O}{A}}$+y$\overrightarrow{{O}{B}}$,且$\overrightarrow{{B}{P}}$=2$\overrightarrow{{P}{A}}$,则$\frac{x}{y}$等于( )

| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | 1 | D. | 2 |
9.设i是虚数单位,则复数i3+$\frac{2}{1-i}$=( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
16.某几何体的正视图,侧视图及俯视图均如图所示,则该几何体的体积为( )


| A. | $\frac{4}{3}$ | B. | $\frac{8}{3}$ | C. | $\sqrt{6}$ | D. | 2$\sqrt{6}$ |
13.设m>1,在约束条件$\left\{\begin{array}{l}{y≥x}\\{x+y≤1}\\{y≤mx+m}\end{array}\right.$下,目标函数z=x+5y的最小值为-8,则m的值为( )
| A. | 3 | B. | $\frac{13}{5}$ | C. | 4 | D. | 8 |
14.函数y=$\frac{x}{x+1}$的图象是( )
| A. |  | B. |  | C. |  | D. | 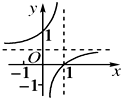 |
 如图,己知E、F、G、H分别是三棱锥A-BCD的棱AB、BC、CD、DA的中点.
如图,己知E、F、G、H分别是三棱锥A-BCD的棱AB、BC、CD、DA的中点. 在三棱锥A-BCD中,底面BCD是正三角形,AC=BD=2,AB=AD=$\sqrt{2}$,O为BC的中点.
在三棱锥A-BCD中,底面BCD是正三角形,AC=BD=2,AB=AD=$\sqrt{2}$,O为BC的中点.