题目内容
13.设m>1,在约束条件$\left\{\begin{array}{l}{y≥x}\\{x+y≤1}\\{y≤mx+m}\end{array}\right.$下,目标函数z=x+5y的最小值为-8,则m的值为( )| A. | 3 | B. | $\frac{13}{5}$ | C. | 4 | D. | 8 |
分析 先画出线性约束条件的可行域,再利用目标函数的几何意义,数形结合先确定最优解,代入直线方程即可得m的值.
解答 解:作出不等式组对应的平面区域如图:
由z=x+5y得y=-$\frac{1}{5}$x+$\frac{z}{5}$,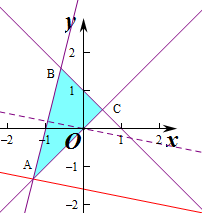
∵m>1,
∴直线y=mx+m=m(x+1)过点且斜率m>1,
平移直线y=-$\frac{1}{5}$x+$\frac{z}{5}$,由图象可知当直线y=-$\frac{1}{5}$x+$\frac{z}{5}$,经过点A时,
直线y=-$\frac{1}{5}$x+$\frac{z}{5}$的截距最小,此时z最小为-8,
即x+5y=-8,
由$\left\{\begin{array}{l}{x+5y=-8}\\{y=x}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=-\frac{4}{3}}\\{y=-\frac{4}{3}}\end{array}\right.$,即A($-\frac{4}{3}$,$-\frac{4}{3}$),
此时A也在直线y=mx+m上,则$-\frac{4}{3}$=m($-\frac{4}{3}$+1)=-$\frac{1}{3}$m,
解得m=4,
故选:C.
点评 本题主要考查线性规划的应用,利用z的几何意义,结合数形结合先确定最优解是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
8. 已知某工厂工人某天加工的零件个数的茎叶图如图所示,那么工人生产的零件个数超过130的比例是( )
已知某工厂工人某天加工的零件个数的茎叶图如图所示,那么工人生产的零件个数超过130的比例是( )
 已知某工厂工人某天加工的零件个数的茎叶图如图所示,那么工人生产的零件个数超过130的比例是( )
已知某工厂工人某天加工的零件个数的茎叶图如图所示,那么工人生产的零件个数超过130的比例是( )| A. | 13.3% | B. | 10% | C. | $\frac{3}{20}$ | D. | $\frac{1}{5}$ |
5.若sinθ=2cosθ,则sin2θ+sinθcosθ-2cos2θ=( )
| A. | $-\frac{4}{3}$ | B. | $\frac{5}{4}$ | C. | $-\frac{3}{4}$ | D. | $\frac{4}{5}$ |