题目内容
(2013·安徽高考)设数列{an}满足a1=2,a2+a4=8,且对任意n∈N*,函数f(x)= x+an+1cos x-an+2sin x满足f′
x+an+1cos x-an+2sin x满足f′ =0.
=0.
(1)求数列{an}的通项公式;
(2)若bn=2 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.
 x+an+1cos x-an+2sin x满足f′
x+an+1cos x-an+2sin x满足f′ =0.
=0.(1)求数列{an}的通项公式;
(2)若bn=2
 ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn.(1)an=n+1 (2)Sn=n2+3n+1-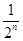
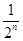
(1)由题设可得f′(x)=an-an+1+an+2-an+1sin x-an+2cos x.
对任意n∈N*,f′ =an-an+1+an+2-an+1=0,
=an-an+1+an+2-an+1=0,
即an+1-an=an+2-an+1,故{an}为等差数列.
由a1=2,a2+a4=8解得{an}的公差d=1,
所以an=2+1·(n-1)=n+1.
(2)由bn=2 =2
=2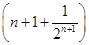 =2n+
=2n+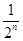 +2知,
+2知,
Sn=b1+b2+…+bn=2n+2·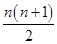 +
+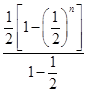 =n2+3n+1-
=n2+3n+1-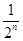 .
.
对任意n∈N*,f′
 =an-an+1+an+2-an+1=0,
=an-an+1+an+2-an+1=0,即an+1-an=an+2-an+1,故{an}为等差数列.
由a1=2,a2+a4=8解得{an}的公差d=1,
所以an=2+1·(n-1)=n+1.
(2)由bn=2
 =2
=2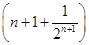 =2n+
=2n+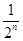 +2知,
+2知,Sn=b1+b2+…+bn=2n+2·
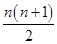 +
+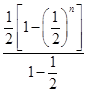 =n2+3n+1-
=n2+3n+1-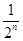 .
.
练习册系列答案
 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
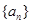 中,
中,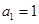 ,对于任意
,对于任意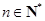 ,都有
,都有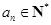 ,
,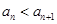 . 设
. 设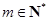 , 记使得
, 记使得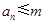 成立的
成立的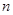 的最大值为
的最大值为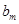 .
.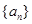 为1,3,5,7,
为1,3,5,7,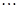 ,写出
,写出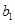 ,
,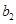 ,
,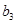 的值;
的值;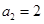 ,求
,求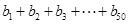 的值;
的值;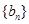 为等差数列,求出所有可能的数列
为等差数列,求出所有可能的数列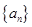 的首项
的首项 ,公差
,公差 ,等比数列
,等比数列 满足
满足
 对任意
对任意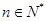 均有
均有 ,求数列
,求数列 .
.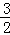 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.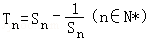 ,求数列{Tn}的最大项的值与最小项的值.
,求数列{Tn}的最大项的值与最小项的值. 的前n项和
的前n项和 ,则
,则 的值为 ( )
的值为 ( ) 中,
中, ,那么
,那么 .
.