题目内容
(2013•天津)已知首项为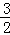 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
(1)求数列{an}的通项公式;
(2)设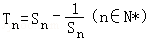 ,求数列{Tn}的最大项的值与最小项的值.
,求数列{Tn}的最大项的值与最小项的值.
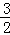 的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.
的等比数列{an}不是递减数列,其前n项和为Sn(n∈N*),且S3+a3,S5+a5,S4+a4成等差数列.(1)求数列{an}的通项公式;
(2)设
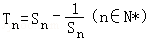 ,求数列{Tn}的最大项的值与最小项的值.
,求数列{Tn}的最大项的值与最小项的值.(1)an=(﹣1)n﹣1•
(2)数列{Tn}的最大项的值为 ,最小项的值为
,最小项的值为

(2)数列{Tn}的最大项的值为
 ,最小项的值为
,最小项的值为
(1)设等比数列的公比为q,
∵S3+a3,S5+a5,S4+a4成等差数列.
∴S5+a5﹣(S3+a3)=S4+a4﹣(S5+a5)
即4a5=a3,
故q2=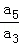 =
=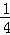
又∵数列{an}不是递减数列,且等比数列的首项为
∴q=﹣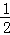
∴数列{an}的通项公式an= ×(﹣
×(﹣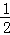 )n﹣1=(﹣1)n﹣1•
)n﹣1=(﹣1)n﹣1•
(2)由(1)得
Sn=1﹣(﹣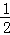 )n=
)n=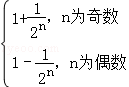
当n为奇数时,Sn随n的增大而减小,所以1<Sn≤S1=
故0<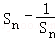 ≤
≤ =
= ﹣
﹣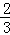 =
=
当n为偶数时,Sn随n的增大而增大,所以1>Sn≥S2=
故0>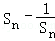 ≥
≥ =
= ﹣
﹣ =
=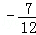
综上,对于n∈N*,总有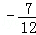 ≤
≤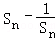 ≤
≤
故数列{Tn}的最大项的值为 ,最小项的值为
,最小项的值为
∵S3+a3,S5+a5,S4+a4成等差数列.
∴S5+a5﹣(S3+a3)=S4+a4﹣(S5+a5)
即4a5=a3,
故q2=
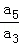 =
=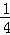
又∵数列{an}不是递减数列,且等比数列的首项为

∴q=﹣
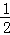
∴数列{an}的通项公式an=
 ×(﹣
×(﹣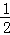 )n﹣1=(﹣1)n﹣1•
)n﹣1=(﹣1)n﹣1•
(2)由(1)得
Sn=1﹣(﹣
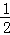 )n=
)n=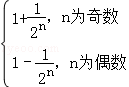
当n为奇数时,Sn随n的增大而减小,所以1<Sn≤S1=

故0<
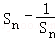 ≤
≤ =
= ﹣
﹣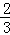 =
=
当n为偶数时,Sn随n的增大而增大,所以1>Sn≥S2=

故0>
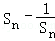 ≥
≥ =
= ﹣
﹣ =
=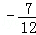
综上,对于n∈N*,总有
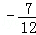 ≤
≤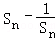 ≤
≤
故数列{Tn}的最大项的值为
 ,最小项的值为
,最小项的值为

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目
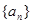 的各项都为正数,
的各项都为正数, 。
。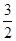 的等差数列,求
的等差数列,求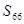 ;
; ,求证:数列
,求证:数列 +f(x),x∈R,且f(1)=
+f(x),x∈R,且f(1)= ,则数列{f(n)}(n∈N*)的前20项的和为( )
,则数列{f(n)}(n∈N*)的前20项的和为( ) x+an+1cos x-an+2sin x满足f′
x+an+1cos x-an+2sin x满足f′ =0.
=0. ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn. 为等差数列
为等差数列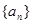 的前
的前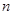 项和,
项和,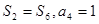 ,求
,求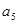 ;
;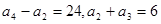 ,求首项
,求首项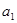 和公比
和公比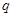
 在动直线
在动直线 上的射影为
上的射影为 ,点
,点 ,则
,则 的最大值是( )
的最大值是( )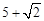


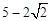
 的前
的前 项和
项和 ,且
,且 的最大值为8,则
的最大值为8,则 ___.
___. 、
、 、
、 、9成等差数列,则
、9成等差数列,则 ____________.
____________.