题目内容
已知{an}是公比为q的等比数列,且am、am+2、am+1成等差数列.
(1)求q的值;
(2)设数列{an}的前n项和为Sn,试判断Sm、Sm+2、Sm+1是否成等差数列?并说明理由.
(1)求q的值;
(2)设数列{an}的前n项和为Sn,试判断Sm、Sm+2、Sm+1是否成等差数列?并说明理由.
(1)q=1或- .(2)当q=1时,Sm , Sm+2 , Sm+1不成等差数列;q=-
.(2)当q=1时,Sm , Sm+2 , Sm+1不成等差数列;q=- 时,Sm , Sm+2 , Sm+1成等差数列.
时,Sm , Sm+2 , Sm+1成等差数列.
 .(2)当q=1时,Sm , Sm+2 , Sm+1不成等差数列;q=-
.(2)当q=1时,Sm , Sm+2 , Sm+1不成等差数列;q=- 时,Sm , Sm+2 , Sm+1成等差数列.
时,Sm , Sm+2 , Sm+1成等差数列.试题分析:(1)根据三数成等差数列,列出等量关系:2am+2=am+1+am ∴2a1qm+1=a1qm+a1qm – 1,在等比数列{an}中,a1≠0,q≠0,∴2q2=q+1,解得q=1或-
 .(2)根据等比数列前n项和公式
.(2)根据等比数列前n项和公式 分类讨论:若q=1,Sm+Sm+1=ma1+(m+1)a1=(2m+1)a1,Sm+2=(m+2)a1∵a1≠0,∴2Sm+2≠S m+Sm+1若q=-
分类讨论:若q=1,Sm+Sm+1=ma1+(m+1)a1=(2m+1)a1,Sm+2=(m+2)a1∵a1≠0,∴2Sm+2≠S m+Sm+1若q=- ,Sm+2=
,Sm+2= ·a1=
·a1= ·a1,Sm+Sm+1=
·a1,Sm+Sm+1= ·a1+
·a1+ ·a1=
·a1= ·a1=
·a1= ·a1,∴2 Sm+2=Sm+Sm+1
·a1,∴2 Sm+2=Sm+Sm+1解:(1)依题意,得2am+2=am+1+am ∴2a1qm+1=a1qm+a1qm – 1
在等比数列{an}中,a1≠0,q≠0,∴2q2=q+1,解得q=1或-
 .
. (2)若q=1,Sm+Sm+1=ma1+(m+1)a1=(2m+1)a1,Sm+2=(m+2)a1
∵a1≠0,∴2Sm+2≠S m+Sm+1
若q=-
 ,Sm+2=
,Sm+2= ·a1=
·a1= ·a1
·a1Sm+Sm+1=
 ·a1+
·a1+ ·a1=
·a1= ·a1
·a1=
 ·a1 ∴2 Sm+2=Sm+Sm+1
·a1 ∴2 Sm+2=Sm+Sm+1故当q=1时,Sm , Sm+2 , Sm+1不成等差数列;q=-
 时,Sm , Sm+2 , Sm+1成等差数列.
时,Sm , Sm+2 , Sm+1成等差数列.
练习册系列答案
 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南师范大学出版社系列答案
同步练习西南师范大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
 x+an+1cos x-an+2sin x满足f′
x+an+1cos x-an+2sin x满足f′ =0.
=0. ,求数列{bn}的前n项和Sn.
,求数列{bn}的前n项和Sn. 在动直线
在动直线 上的射影为
上的射影为 ,点
,点 ,则
,则 的最大值是( )
的最大值是( )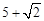


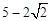
 的前
的前 项和
项和 ,且
,且 的最大值为8,则
的最大值为8,则 ___.
___. 的前
的前 项和为
项和为 ,已知
,已知 ,且
,且 ,则下列结论中正确的有 .(填序号)
,则下列结论中正确的有 .(填序号) ;
; ;
; 是数列
是数列 是数列
是数列 中的最小项.
中的最小项. 成等差数列,则m=________.
成等差数列,则m=________.