题目内容
20. 如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=2$\sqrt{3}$,则PC与平面PAD所成角的大小为45°.
如图,四棱锥P-ABCD的底面ABCD是矩形,PA⊥平面ABCD,PA=AD=2,BD=2$\sqrt{3}$,则PC与平面PAD所成角的大小为45°.
分析 由PA⊥平面ABCD,即可得到CD⊥PA,CD⊥AD,从而根据线面垂直的判定定理即可得到CD⊥平面PAD,从而∠CPD便是PC和平面PAD所成角,根据已知的边长度即可求得CD=PD,从而得出∠CPD=45°.
解答 解:PA⊥平面ABCD,CD?平面ABCD;
∴CD⊥PA;
又CD⊥AD,AD∩PA=A;
∴CD⊥平面PAD;
∴∠CPD是直线PC和平面PAD所成角;
PD=$\sqrt{P{A}^{2}+A{D}^{2}}$=2$\sqrt{2}$,CD=AB=$\sqrt{B{D}^{2}-A{D}^{2}}=2\sqrt{2}$;
∴∠CPD=45°.
故答案为:45°.
点评 考查线面垂直的性质及判定定理,线面角的概念及求法,直角三角形边的关系.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
8.已知过双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的中心的直线交双曲线于点A,B,在双曲线C上任取与点A,B不重合的点P,记直线PA,PB,AB的斜率分别为k1,k2,k,若k1k2>k恒成立,则离心率e的取值范围为( )
| A. | 1<e<$\sqrt{2}$ | B. | 1<e≤$\sqrt{2}$ | C. | e>$\sqrt{2}$ | D. | e≥$\sqrt{2}$ |
12.已知角α的终边在函数y=-|x|的图象上,则cosα的值为( )
| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\frac{\sqrt{2}}{2}$ | C. | $±\frac{\sqrt{2}}{2}$ | D. | $\frac{1}{2}$ |
10.已知数列{an}满足2an+1+an=0,a2=1,则{an}的前9项和等于( )
| A. | -$\frac{2}{3}$(1-2-9) | B. | $\frac{1}{3}$(1-2-9) | C. | -$\frac{4}{3}$(1+2-9) | D. | (1-2-9) |
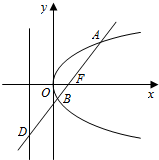 已知F为抛物线y2=4x的焦点,过点F引一条直线与抛物线交于A、B两点,与抛物线准线交于D点.
已知F为抛物线y2=4x的焦点,过点F引一条直线与抛物线交于A、B两点,与抛物线准线交于D点. 已知椭圆C的中心在原点O,焦点在x轴上,离心率为$\frac{1}{2}$,右焦点到右顶点的距离为1
已知椭圆C的中心在原点O,焦点在x轴上,离心率为$\frac{1}{2}$,右焦点到右顶点的距离为1 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴为4,离心率e=$\frac{\sqrt{3}}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的长轴为4,离心率e=$\frac{\sqrt{3}}{2}$.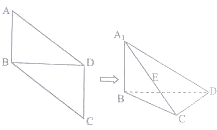 如图,在平行四边形ABCD中,AB=1,BD=$\sqrt{2}$,∠ABD=90°,将△ABD沿对角线BD折起,折后的点A变为A1,且A1C=2.
如图,在平行四边形ABCD中,AB=1,BD=$\sqrt{2}$,∠ABD=90°,将△ABD沿对角线BD折起,折后的点A变为A1,且A1C=2.