题目内容
14.已知矩阵A=$[\begin{array}{l}{1}&{-2}\\{-2}&{-1}\end{array}]$,B=$[\begin{array}{l}{5}\\{-15}\end{array}]$满足AX=B,求矩阵X.分析 由AX=B,得$[\begin{array}{l}{1}&{-2}\\{-2}&{-1}\end{array}]$$[\begin{array}{l}{a}\\{b}\end{array}]$=$[\begin{array}{l}{5}\\{-15}\end{array}]$,求解即可.
解答 解:设x=$[\begin{array}{l}{a}\\{b}\end{array}]$,由$[\begin{array}{l}{1}&{-2}\\{-2}&{-1}\end{array}]$$[\begin{array}{l}{a}\\{b}\end{array}]$=$[\begin{array}{l}{5}\\{-15}\end{array}]$
得$\left\{\begin{array}{l}{a-2b=5}\\{-2a-b=-15}\end{array}\right.$解得$\left\{\begin{array}{l}{a=7}\\{b=1}\end{array}\right.$
此时x=$[\begin{array}{l}{7}\\{1}\end{array}]$
点评 本题主要考查了矩阵的应用,属于基础题型.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
1.已知椭圆M:$\frac{{x}^{2}}{4}$+y2=1的上、下顶点为A,B,过点P(0,2)的直线l与椭圆M相交于两个不同的点C,D(C在线段PD之间),则$\overrightarrow{OC}$•$\overrightarrow{OD}$的取值范围( )
| A. | (-1,16) | B. | [-1,16] | C. | (-1,$\frac{13}{4}$) | D. | [-1,$\frac{13}{4}$) |
6.已知sinα+cos(π-α)=$\frac{1}{3}$,则sin2α的值为( )
| A. | $\frac{8}{9}$ | B. | $\frac{1}{9}$ | C. | $-\frac{8}{9}$ | D. | $\frac{4}{9}$ |
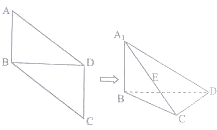 如图,在平行四边形ABCD中,AB=1,BD=$\sqrt{2}$,∠ABD=90°,将△ABD沿对角线BD折起,折后的点A变为A1,且A1C=2.
如图,在平行四边形ABCD中,AB=1,BD=$\sqrt{2}$,∠ABD=90°,将△ABD沿对角线BD折起,折后的点A变为A1,且A1C=2.