题目内容
9.已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的左、右焦点分别为F1,F2,过点(1,$\frac{{\sqrt{2}}}{2}$),离心率e=$\frac{{\sqrt{2}}}{2}$.(1)求椭圆的标准方程;
(2)过点F1的直线l与该椭圆交于M,N两点,且|${\overrightarrow{{F_2}M}$+$\overrightarrow{{F_2}N}}$|=$\frac{{2\sqrt{26}}}{3}$,求直线l的方程.
分析 (1)根据椭圆的离心率和定点坐标,代入求出a,b,即可求椭圆的标准方程;
(2)设出直线方程,联系直线和椭圆,利用根与系数之间的关系进行求解即可.
解答 解:(1)由已知得$\left\{{\begin{array}{l}{\frac{c}{a}=\frac{{\sqrt{2}}}{2}}\\{\frac{1}{a^2}+\frac{1}{{2{b^2}}}=1}\\{{c^2}={a^2}+{b^2}}\end{array}}\right.$,解得a2=2,b2=1,
故所求椭圆的方程为$\frac{x^2}{2}+{y^2}=1$…(4分)
(2)由(1)得F1(-1,0),F2(1,0)
①若直线l的斜率不存在,则直线l的方程为x=-1,由$\left\{{\begin{array}{l}{x=-1}\\{\frac{x^2}{2}+{y^2}=1}\end{array}}\right.$得$y=±\frac{{\sqrt{2}}}{2}$.
设$M(-1,\frac{{\sqrt{2}}}{2}),N(-1,-\frac{{\sqrt{2}}}{2})$
∴$|{\overrightarrow{{F_2}M}+\overrightarrow{{F_2}N}}|=|{({-2,\frac{{\sqrt{2}}}{2}})+({-2,-\frac{{\sqrt{2}}}{2}})}|=|{(-4,0)}|=4$这与已知相矛盾;…(6分)
②若直线l的斜率存在,设直线l的斜率为k,则直线l的方程为y=k(x+1).
设M(x1,y1),N(x2,y2),
联立$\left\{{\begin{array}{l}{y=k({x+1})}\\{\frac{x^2}{2}+{y^2}=1}\end{array}}\right.$,消元得(1+2k2)x2+4k2x+2k2-2=0,
∴${x_1}+{x_2}=\frac{{-4{k^2}}}{{1+2{k^2}}},{x_1}{x_2}=\frac{{2{k^2}-2}}{{1+2{k^2}}}$,
∴所以${y_1}+{y_2}=k({x_1}+{x_2}+2)=\frac{2k}{{1+2{k^2}}}$…(10分)
又∵$\overrightarrow{{F_2}M}=({x_1}-1,{y_1}),\overrightarrow{{F_2}N}=({x_2}-1,{y_2})$
∴$\overrightarrow{{F_2}M}+\overrightarrow{{F_2}N}=({x_1}+{x_2}-2,{y_1}+{y_2})$
∴$|{\overrightarrow{{F_2}M}+\overrightarrow{{F_2}N}}|=\sqrt{{{({x_1}+{x_2}-2)}^2}+{{({y_1}+{y_2})}^2}}=\sqrt{{{({\frac{{8{k^2}+2}}{{1+2{k^2}}}})}^2}+{{({\frac{2k}{{1+2{k^2}}}})}^2}}=\frac{{2\sqrt{26}}}{3}$
化简得40k4-23k2-17=0,
解得k2=1或${k^2}=-\frac{17}{40}$(舍去),
∴k=±1,
故所求直线l的方程为y=x+1或y=-x-1…(12分)
点评 本题主要考查椭圆的方程以及直线和椭圆的位置关系的应用,利用消元法转化为一元二次方程形式是解决本题的关键.

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案| A. | -$\frac{3}{4}$ | B. | -$\frac{9}{16}$ | C. | -$\frac{4}{3}$ | D. | -$\frac{16}{9}$ |
| A. | 有99%的人认为该栏目优秀 | |
| B. | 有99%的人认为该栏目是否优秀与改革有关系 | |
| C. | 有99%的把握认为电视栏目是否优秀与改革有关系 | |
| D. | 没有理由认为电视栏目是否优秀与改革有关系 |
| A. | {x|x<$\frac{1}{2}$} | B. | {x|x<$\frac{1}{2}$且x≠-$\frac{1}{2}$} | C. | {x|x>$\frac{1}{2}$} | D. | {x|x≤$\frac{1}{2}$且x≠-$\frac{1}{2}$} |
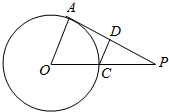 过⊙O外一点P作⊙O的切线PA,切点为A,连OP与⊙O交于点C,过C作AP的垂线,垂足为D,若PA=8cm,PC=4cm,则PD的长为3.2.
过⊙O外一点P作⊙O的切线PA,切点为A,连OP与⊙O交于点C,过C作AP的垂线,垂足为D,若PA=8cm,PC=4cm,则PD的长为3.2.