题目内容
19.已知点M(3,1),直线ax-y+4=0及圆C:(x-1)2+(y-2)2=4(1)若直线ax-y+4=0与圆C相切,求a的值;
(2)若直线ax-y+4=0与圆C相交于A,B两点,且弦AB的长为2$\sqrt{3}$,求a的值;
(3)求过点M的圆C的切线方程.
分析 (1)根据直线和圆相切的关系即可求a的值;
(2)根据直线和圆相交,以及弦长公式即可求a的值;
(3)根据直线和圆相切的关系即可
解答 解:(1)圆心坐标C(1,2),半径R=2,
若若直线ax-y+4=0与圆C相切,
则圆心到直线的距离d=$\frac{|a-2+4|}{\sqrt{1+{a}^{2}}}$=$\frac{|a+2|}{\sqrt{1+{a}^{2}}}$=2,
解得a=0或a=$\frac{4}{3}$…(4分)
(2)∵圆心到直线ax-y+4=0的距离为d═$\frac{|a-2+4|}{\sqrt{1+{a}^{2}}}$=$\frac{|a+2|}{\sqrt{1+{a}^{2}}}$
∴($\frac{|a+2|}{\sqrt{1+{a}^{2}}}$)2+($\frac{2\sqrt{3}}{2}$)2=4,
解得a=-$\frac{3}{4}$…(8分)
(3)圆心C(1,2),半径为r=2
当直线的斜率不存在时,直线方程为x=3,
由圆心C(1,2)到直线x=3的距离d=3-1=2=r知,
直线与圆相切.
当直线的斜率存在时,设方程y-1=k(x-3)
即kx-y+1-3k=0
由题意知$\frac{|k-2+1-3k|}{\sqrt{1+{k}^{2}}}$=2,解得k=$\frac{3}{4}$,
即直线方程为y-1=$\frac{3}{4}$(x-3),
即3x-4y-5=0,
综上所述,过M点的圆的切线方程为x=3或3x-4y-5=0…(14分)
点评 本题主要考查直线和圆的位置关系的应用,根据点到直线的距离公式以及相交弦长公式是解决本题的关键.

练习册系列答案
相关题目
11.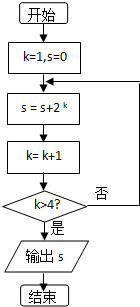 执行如图所示的程序框图,则输出s的值为( )
执行如图所示的程序框图,则输出s的值为( )
 执行如图所示的程序框图,则输出s的值为( )
执行如图所示的程序框图,则输出s的值为( )| A. | 30 | B. | 31 | C. | 62 | D. | 63 |