题目内容
19.已知直线y=kx+1与圆x2+y2-kx-my-5=0交于M,N两点,且M,N关于直线x+y=0对称,若P(a,b)为平面区域$\left\{\begin{array}{l}{kx-my-3≤0}\\{kx-y+1≤0}\\{x≥0}\end{array}\right.$上的任意一点,则$\frac{b+1}{a+1}$的最大值是4.分析 先求出m,k,再利用区域,求出$\frac{b+1}{a+1}$的最大值.
解答 解:由题意可知,直线x+y=0过圆心,且与直线y=kx+1垂直,
∴k=1,
圆x2+y2-kx-my-5=0的圆心坐标($\frac{1}{2}$,$\frac{m}{2}$)在直线x+y=0上,所以m=-1,
平面区域$\left\{\begin{array}{l}{kx-my-3≤0}\\{kx-y+1≤0}\\{x≥0}\end{array}\right.$为$\left\{\begin{array}{l}{x+y-3≤0}\\{x-y+1≤0}\\{x≥0}\end{array}\right.$,
$\frac{b+1}{a+1}$表示区域内的点(a,b),与(-1,-1)连线的斜率,由图形可得(0,3)处取得最大值4,
故答案为:4
点评 本题考查对称知识,圆的一般方程,考查线性规划知识,考查学生分析解决问题的能力,是中档题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
10.甲、乙两人为了响应政府“节能减排”的号召,决定购置某品牌空调各一台.经了解,目前市场上销售此品牌空调有A,B,C三种型号,甲从A,B,C三类型号中挑选,乙从B,C两种型号中挑选,甲、乙二人选择各类车型的概率如下表:
若甲、乙都选C型号的概率为$\frac{3}{10}$.
(1)求p,q的值;
(2)某市对购买此品牌空调进行补贴,补贴标准如下表:
记甲、乙两人购空调所获得财政补贴的和为X,求X的分布列和期望.
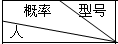 | A | B | C |
| 甲 | $\frac{1}{5}$ | p | q |
| 乙 |  | $\frac{1}{4}$ | $\frac{3}{4}$ |
(1)求p,q的值;
(2)某市对购买此品牌空调进行补贴,补贴标准如下表:
| 型号 | A | B | C |
| 补贴金额(百元/台) | 3 | 4 | 5 |
14.设函数f′(x)的偶函数f(x)(x∈R且x≠0)的导函数,f(2)=0且当x>0时,xf′(x)-f(x)>0,则使f(x)<0成立的x的取值范围为( )
| A. | (-∞,-2)∪(0,2) | B. | (-2,0)∪(0,2) | C. | (-2,0)∪(2,+∞) | D. | (-∞,-2)∪(2,+∞) |
8.有5道题中,有3道理科题和2道文科题,如果不放回地依次抽取2道题,则在第1次抽到理科题的条件下,第2次抽到理科题的概率为( )
| A. | $\frac{3}{5}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{5}$ | D. | $\frac{3}{10}$ |
9.若直线2x+3y-1=0与直线4x+my+11=0平行,则它们之间的距离为( )
| A. | $\frac{{\sqrt{13}}}{2}$ | B. | $\frac{{2\sqrt{13}}}{13}$ | C. | $\frac{{6\sqrt{13}}}{13}$ | D. | $\frac{{12\sqrt{13}}}{13}$ |