题目内容
10.甲、乙两人为了响应政府“节能减排”的号召,决定购置某品牌空调各一台.经了解,目前市场上销售此品牌空调有A,B,C三种型号,甲从A,B,C三类型号中挑选,乙从B,C两种型号中挑选,甲、乙二人选择各类车型的概率如下表: | A | B | C |
| 甲 | $\frac{1}{5}$ | p | q |
| 乙 |  | $\frac{1}{4}$ | $\frac{3}{4}$ |
(1)求p,q的值;
(2)某市对购买此品牌空调进行补贴,补贴标准如下表:
| 型号 | A | B | C |
| 补贴金额(百元/台) | 3 | 4 | 5 |
分析 (1)仔细阅读表格得出方程组$\left\{\begin{array}{l}\frac{3}{4}q=\frac{3}{10}\\ p+q+\frac{1}{5}=1\end{array}\right.$,求解即可.
(2)确定随机变量X可能取值为7,8,9,10.求解相应的概率,列出分布列,再运用数学期望公式求解即可.
解答 解:(1)由题意得$\left\{\begin{array}{l}\frac{3}{4}q=\frac{3}{10}\\ p+q+\frac{1}{5}=1\end{array}\right.$所以$p=\frac{2}{5},q=\frac{2}{5}$.
(2)X可能取值为7,8,9,10.
$P(X=7)=\frac{1}{5}×\frac{1}{4}=\frac{1}{20}$,$P(X=8)=\frac{1}{5}×\frac{3}{4}+\frac{2}{5}×\frac{1}{4}=\frac{1}{4}$,$P(X=9)=\frac{2}{5}×\frac{1}{4}+\frac{2}{5}×\frac{3}{4}=\frac{2}{5}$; $P(X=10)=\frac{2}{5}×\frac{3}{4}=\frac{3}{10}$.
所以X的分布列为:
| X | 7 | 8 | 9 | 10 |
| P | $\frac{1}{20}$ | $\frac{1}{4}$ | $\frac{2}{5}$ | $\frac{3}{10}$ |
点评 考察了图表格的运用,分析能力,计算化简能力,属于难题,关键是掌握好随机变量的概率的关系,列出方程组.

练习册系列答案
 一本好题口算题卡系列答案
一本好题口算题卡系列答案
相关题目
2.已知α的终边在第一象限,则角$\frac{α}{2}$的终边在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第一或第三象限 | D. | 第一或第四象限 |
20.袋中有白球2个,红球3个,从中任取两个,则互斥且不对立的两个事件是( )
| A. | 至少有一个白球;都是白球 | B. | 两个白球;至少有一个红球 | ||
| C. | 红球、白球各一个;都是白球 | D. | 红球、白球各一个;至少有一个白球 |
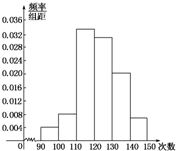 为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.
为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.