题目内容
7.(Ⅰ)运用S(α+β)及C(α+β)证明:tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$;(Ⅱ)在△ABC中,证明tanA+tanB+tanC=tanAtanBtanC.
分析 (Ⅰ)由条件利用同角三角函数的基本关系、两角和差的三角公式化简tan(α+β),即可证得结论.
(Ⅱ)△ABC中,由tanA=-tan(B+C) 利用两角和差的正切公式,求得tanB+tanC=-tanA+tanAtanBtanC,代入要证等式的左边,即可证得结论.
解答 (Ⅰ)证明:∵tan(α+β)=$\frac{sin(α+β)}{cos(α+β)}$=$\frac{sinαcosβ+cosαsinβ}{cosαcosβ-sinαsinβ}$=$\frac{\frac{sinαcosβ}{cosαcosβ}+\frac{cosαsinβ}{cosαcosβ}}{1-\frac{sinαsinβ}{cosαcosβ}}$=$\frac{tanα+tanβ}{1-tanαtanβ}$,
∴tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$.
(Ⅱ)证明:△ABC中,tanA=-tan(B+C)=-$\frac{tanB+tanC}{1-tanBtanC}$,
∴tanB+tanC=-tanA+tanAtanBtanC,
∴tanA+tanB+tanC=tanA-tanA+tanAtanBtanC=tanAtanBtanC,
∴tanA+tanB+tanC=tanAtanBtanC成立.
点评 本题主要考查同角三角函数的基本关系,两角和差的三角公式,属于基础题.

练习册系列答案
相关题目
17.已知函数y=$\frac{1}{x}$的导数为y′,y′=( )
| A. | -$\frac{1}{x}$ | B. | $\frac{1}{x}$ | C. | -$\frac{1}{{x}^{2}}$ | D. | -1 |
2.已知α的终边在第一象限,则角$\frac{α}{2}$的终边在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第一或第三象限 | D. | 第一或第四象限 |
12.(2-x)10=a0+a1x+a2x2+…+a10x10.则a1+a2+a3+…+a10=( )
| A. | 1 | B. | -1 | C. | 1023 | D. | -1023 |
17.设(2x-1)5=a0+a1(x-1)+a2(x-1)2+…+a5(x-1)5,则a0+a1+a2+…+a5的值为( )
| A. | 1 | B. | -1 | C. | 243 | D. | -243 |
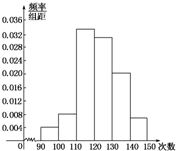 为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.
为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.