题目内容
4.已知复数z1=$\frac{1}{a+2}$+(a2-1)i,z2=2+2(a+1)i(a∈R,i是虚数单位).(1)若复数z1-z2在复平面上对应点落在第一象限,求实数a的取值范围;
(Ⅱ)若虚数z1是实系数一元二次方程4x2-4x+m=0的根,求实数m值.
分析 (1)由复数对应的点在第一象限得到实部大于0,虚部大于0,解不等式组即可;
(Ⅱ)利用z1是实系数一元二次方程4x2-4x+m=0的根,得到另一个根是复数z1的共轭复数,利用根与系数的关系得到a和m.
解答 解:(Ⅰ由已知得到z1-z2=$\frac{1}{a+2}$-2+(a2-2a-3)i,因为在复平面上对应点落在第一象限,所以$\left\{\begin{array}{l}{\frac{1}{a+2}-2>0}\\{{a}^{2}-2a-3>0}\end{array}\right.$,解得$\left\{\begin{array}{l}{-2<a<-\frac{3}{2}}\\{a>3或a<-1}\end{array}\right.$,所以$-2<a<-\frac{3}{2}$;
(Ⅱ)因为虚数z1是实系数一元二次方程4x2-4x+m=0的根,所以$\overline{z}$1是方程的另一个根,所以${z}_{1}+\overline{{z}_{1}}=\frac{2}{a+2}$=1,所以a=0,
所以${z}_{1}=\frac{1}{2}-i$,$\overline{{z}_{1}}=\frac{1}{2}+i$,
所以${z}_{1}•\overline{{z}_{1}}=\frac{m}{4}=\frac{5}{4}$,所以m=5.
点评 本题考查了复数的几何意义以及实系数的一元二次方程由虚数根时,根互为共轭复数的运用.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.圆O1:x2+y2+6x-4y+10=0与圆O2:x2+y2=4的位置关系是( )
| A. | 相离 | B. | 相交 | C. | 外切 | D. | 内切 |
12.(2-x)10=a0+a1x+a2x2+…+a10x10.则a1+a2+a3+…+a10=( )
| A. | 1 | B. | -1 | C. | 1023 | D. | -1023 |
9.在四边形ABCD中,若$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}$,且$|{\overrightarrow{AB}}|=|{\overrightarrow{AD}}|$,则( )
| A. | ABCD是矩形 | B. | ABCD是菱形 | ||
| C. | ABCD是正方形 | D. | ABCD是平行四边形 |
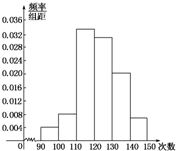 为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.
为了了解高一学生的体能情况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形面积之比为2:4:17:15:9:3,第二小组频数为12.