题目内容
【题目】已知函数f（x）= 
（e为自然对数的底数，e=2.71828…）．
（1）证明：函数f（x）为奇函数；
（2）判断并证明函数f（x）的单调性，再根据结论确定f（m2﹣m+1）+f（﹣ 
）与0的大小关系；
（3）是否存在实数k，使得函数f（x）在定义域[a，b]上的值域为[kea ， keb]．若存在，求出实数k的取值范围；若不存在，请说明理由．
【答案】
（1）证明：函数f（x）定义域为R，
对于任意的x∈R，都有f（﹣x）= 
= 
=﹣f（x），
所以函数f（x）为奇函数
（2）解：f（x）= 
在R上为增函数，理由如下：
∵f′（x）= 
＞0恒成立，
∴f（x）= 在R上为增函数，
∵ 
∴f（m2﹣m+1）≥f（﹣ 
）=﹣f（ ），
∴f（m2﹣m+1）+f（﹣ ）≥0
（3）∵f（x）为R上的增函数且函数f（x）在定义域[a，b]上的值域为[kea，keb]．
∴k＞0且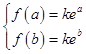 
，
=kex在R上有两个不等实根；
令t=ex，t＞0且单调增，问题即为方程kt2+（k﹣1）t+1=0在（0，+∞）上有两个不等实根，
设h（t）=kt2+（k﹣1）t+1，
则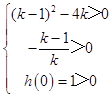 
，解得：0＜k＜3﹣2 
【解析】（1）根据奇函数的定义，可判断函数f（x）为奇函数；（2）f（x）= 
在R上为增函数，利用导数法可证明结论，进而判断出f（m2﹣m+1）+f（﹣ 
）≥0；（3）若函数f（x）在定义域[a，b]上的值域为[kea，keb]．则 =kex在R上有两个不等实根，进而得到实数k的取值范围．
【考点精析】认真审题，首先需要了解函数的图象(函数的图像是由直角坐标系中的一系列点组成；图像上每一点坐标（x，y）代表了函数的一对对应值，他的横坐标x表示自变量的某个值，纵坐标y表示与它对应的函数值)，还要掌握利用导数研究函数的单调性(一般的,函数的单调性与其导数的正负有如下关系： 在某个区间
内，(1)如果
，那么函数
在这个区间单调递增；(2)如果
，那么函数
在这个区间单调递减)的相关知识才是答题的关键．
