题目内容
【题目】设函数f（x）=|ax﹣x2|+2b（a，b∈R）．
（1）当a=﹣2，b=﹣ 
时，解方程f（2x）=0；
（2）当b=0时，若不等式f（x）≤2x在x∈[0，2]上恒成立，求实数a的取值范围；
（3）若a为常数，且函数f（x）在区间[0，2]上存在零点，求实数b的取值范围．
【答案】
（1）解：当a=﹣2，b=﹣ 
时，f（x）=|x2+2x|﹣15，所以方程即为：|2x（2x+2）|=15
解得：2x=3或2x=﹣5（舍），所以x= 
（2）解：当b=0时，若不等式：x|a﹣x|≤2x
在x∈[0，2]上恒成立；
当x=0时，不等式恒成立，则a∈R；
当0＜x≤2时，则|a﹣x|≤2，
在[0，22]上恒成立，即﹣2≤x﹣a≤2在（0，2]上恒成立，
因为y=x﹣a在（0，2]上单调增，ymax=2﹣a，ymin=﹣a，则 
，解得：0≤a≤2；
则实数a的取值范围为[0.2]
（3）解：函数f（x）在[0，2]上存在零点，即方程x|a﹣x|=﹣2b在[0，2]上有解；
设h（x）=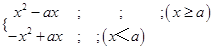 
当a≤0时，则h（x）=x2﹣ax，x∈[0，2]，且h（x）在[0，2]上单调增，
所以h（x）min=h（0）=0，h（x）max=h（2）=4﹣2a，
则当 
0≤﹣2b≤4﹣2a时，原方程有解，则a﹣2≤b≤0；
当a＞0时，h（x）= ，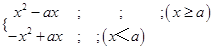
h（x）在[0， 
]上单调增，在[ 
]上单调减，在[a，+∞）上单调增；
①当 
，即a≥4时，h（x）min=h（0）=0，h（x）max=h（2）=4﹣2a，
则当则当0≤﹣2b≤2a﹣4时，原方程有解，则2﹣a≤b≤0；
②当 
，即2≤a＜4时，h（x）min=h（0）=0，h（x）max=h（ ）= ，
则当0≤﹣2b≤ 时，原方程有解，则﹣ 
；
③当0＜a＜2时，h（x）min=h（0）=0，h（x）max=max{h（2），h（ ）=max{4﹣2a， }
当 
，即当﹣4+4 
≤a＜2时，h（x）max= 
，则当0≤﹣2b≤ 时，原方程有解，则 
；
当 
，即则0 
时，h（x）max=4﹣2a，
则当0≤﹣2b≤4﹣2a时，原方程有解，则a﹣2≤b≤0；
综上，当0＜a＜﹣4+4 时，实数b的取值范围为[a﹣2，0]；
当﹣4+4 ≤a＜4时，实数b的取值范围为[ 
]；
当a≥4时，实数b的取值范围为[2﹣a，0]
【解析】（1）解：（1）原方程即为：|2x（2x+2）|=15，解得2x即可，（2）不等式f（x）≤2x在x∈[0，2]上恒成立，及（f（x）﹣2x）max≤在x∈[0，2]上恒成立即可‘（3）函数f（x）在[0，2]上存在零点，即方程x|a﹣x|=﹣2b在[0，2]上有解，分类求出设h（x）= 
的值域即可．
