题目内容
【题目】已知函数f（x）=（ 
）x的图象与函数y=g（x）的图象关于直线y=x对称．
（1）若f（g（x））=6﹣x2 ， 求实数x的值；
（2）若函数y=g（f（x2））的定义域为[m，n]（m≥0），值域为[2m，2n]，求实数m，n的值；
（3）当x∈[﹣1，1]时，求函数y=[f（x）]2﹣2af（x）+3的最小值h（a）．
【答案】
（1）解：∵函数f（x）=（ 
）x的图象与函数y=g（x）的图象关于直线y=x对称，
∴g（x）= 
，
∵f（g（x））=6﹣x2，
∴ 
=6﹣x2=x，
即x2+x﹣6=0，
解得x=2或x=﹣3（舍去），
故x=2，
（2）解：y=g（f（x2））= 
=x2，
∵定义域为[m，n]（m≥0），值域为[2m，2n]，
，
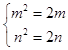解得m=0，n=2，
（3）解：令t=（ ）x，
∵x∈[﹣1，1]，
∴t∈[ ，2]，
则y=[f（x）]2﹣2af（x）+3等价为y=m（t）=t2﹣2at+3，
对称轴为t=a，
当a＜ 时，函数的最小值为h（a）=m（ ）= 
﹣a；
当 ≤a≤2时，函数的最小值为h（a）=m（a）=3﹣a2；
当a＞2时，函数的最小值为h（a）=m（2）=7﹣4a；
故h（a）=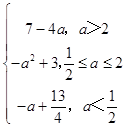 
【解析】（1）根据函数的对称性即可求出g（x），即可得到f（g（x））=x，解得即可．（2）先求出函数的解析式，得到 
，解得m=0，n=2，（3）由x∈[﹣1，1]可得t∈[ 
，2]，结合二次函数的图象和性质，对a进行分类讨论，即可得到函数y=f2（x）﹣2af（x）+3的最小值h（a）的表达式．
【考点精析】本题主要考查了函数的最值及其几何意义的相关知识点，需要掌握利用二次函数的性质（配方法）求函数的最大（小）值；利用图象求函数的最大（小）值；利用函数单调性的判断函数的最大（小）值才能正确解答此题．
