题目内容
【题目】选修4—5;不等式选讲.
已知函数![]() .
.
(1)若![]() 的解集非空,求实数
的解集非空,求实数![]() 的取值范围;
的取值范围;
(2)若正数![]() 满足
满足![]() ,
, ![]() 为(1)中m可取到的最大值,求证:
为(1)中m可取到的最大值,求证: ![]() .
.
【答案】(1) ![]() ;(2)见解析.
;(2)见解析.
【解析】试题分析:(1)讨论三种情况去绝对值符号,可得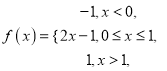 所以
所以![]() ,由此得
,由此得![]() ,解得
,解得![]() ;(2)利用分析法,由(1)知,
;(2)利用分析法,由(1)知, ![]() ,所以
,所以![]() ,因为
,因为![]() ,要证
,要证![]() ,只需证
,只需证![]() ,即证
,即证![]() ,只需证
,只需证![]() 即可得结果.
即可得结果.
试题解析:(1)去绝对值符号,可得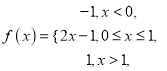
所以![]() ,
,
所以![]() ,解得
,解得![]() ,
,
所以实数![]() 的取值范围为
的取值范围为![]() 。
。
(2)由(1)知, ![]() ,所以
,所以![]() 。
。
因为![]() ,
,
所以要证![]() ,只需证
,只需证![]() ,
,
即证![]() ,即证
,即证![]() .
.
因为![]() ,所以只需证
,所以只需证![]() ,
,
因为![]() ,∴
,∴![]() 成立,所以
成立,所以![]()
解法二:x2+y2=2,x、y∈R+,x+y≥2xy ![]()
设: 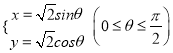
证明:x+y-2xy= ![]()
= ![]()
令![]()
![]() ,
, ![]() ∴
∴![]()
![]()
![]() 原式=
原式=![]()
=![]()
=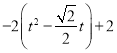
=![]()
当![]() 时,
时, ![]()
![]()
![]()

练习册系列答案
相关题目