Question

【题目】选修4－4：坐标系与参数方程

在平面直角坐标系中，曲线的参数方程为（为参数，且），以为极点， 轴的正半轴为极轴，建立极坐标系，直线 的极坐标方程为．

（1）若曲线与只有一个公共点，求的值；

（2）， 为曲线上的两点，且，求△的面积最大值．

Answer 1

【答案】(1)a=1;(2)见解析.

【解析】试题分析：（1）根据曲线的参数方程可得曲线是以为圆心，以为半径的圆，再将直线的极坐标方程化为直角坐标方程，根据曲线与只有一个公共点，由圆心到直线的距离等于半径，即可求得的值；（2）法一：由题意，曲线的极坐标方程为设的极角为， 的极角为，即可表示出，根据积化和差公式及三角函数图象即可求得△的面积最大值；法二：根据曲线是圆及，利用正弦定理可得，再根据余弦定理与基本不等式即可求得的最大值，从而可得△的面积最大值.

试题解析：（1）由题意可得曲线是以为圆心，以为半径的圆；

直线的直角坐标方程为.

由直线与圆只有一个公共点，则可得.

∴（舍）或

∴

（2）法一：由题意，曲线的极坐标方程为.

设的极角为， 的极角为，则：

∵

∴当时， 取得最大值为.

∴的面积最大值为．

法二：∵曲线是以为圆心，以为半径的圆，且.

∴由正弦定理得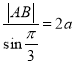： ，即.

∴由余弦定理得： ，则： ，当且仅当时取等号．

∴的面积最大值为．