题目内容
【题目】已知椭圆C的中心在原点,焦点在x轴上,以两个焦点和短轴的两个端点为顶点的四边形是一个面积为8的正方形(记为Q).
(Ⅰ)求椭圆C的方程;
(Ⅱ)设点P是直线x=﹣4与x轴的交点,过点P的直线l与椭圆C相交于M,N两点,当线段MN的中点落在正方形Q内(包括边界)时,求直线l斜率的取值范围.
【答案】
【解析】试题分析:(I)设出椭圆的方程,根据正方形的面积求出椭圆中参数a的值且判断出参数b,c的关系,根据椭圆的三个参数的关系求出b,c的值得到椭圆的方程.
(II)设出直线的方程,将直线的方程与椭圆方程联立,利用二次方程的韦达定理得到弦中点的坐标,根据中点在正方形的内部,得到中点的坐标满足的不等关系,求出k的范围.
解:(Ⅰ)依题意,设椭圆C的方程为![]() ,焦距为2c,
,焦距为2c,
由题设条件知,a2=8,b=c
所以![]() =4,
=4,
故椭圆的方程为![]() ;
;
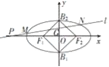
(II)椭圆C的左准线方程为x=﹣4,所以点P的坐标为(﹣4,0)
显然直线l的斜率存在,所以设直线l的方程为y=k(x+4)
设点M,N的坐标分别为(x1,y1),(x2,y2),线段MN的中点为G(x0,y0)
由直线代入椭圆方程得(1+2k2)x2+16k2x+32k2﹣8=0.①
由△=(16k2)2﹣4(1+2k2)(32k2﹣8)>0解得﹣![]() <k<
<k<![]() .②
.②
因为x1,x2是方程①的两根,
所以x1+x2=﹣![]() ,于是x0=
,于是x0=![]() =﹣
=﹣![]() ,y0=
,y0=![]() .
.
因为x0=![]() =﹣
=﹣![]() ≤0,所以点G不可能在y轴的右边,
≤0,所以点G不可能在y轴的右边,
又直线F1B2,F1B1方程分别为y=x+2,y=﹣x﹣2
所以点G在正方形Q内(包括边界)的充要条件为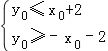 ,即
,即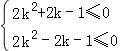
解得![]() ,此时②也成立.
,此时②也成立.
故直线l斜率的取值范围是![]() .
.

【题目】从某食品厂生产的面包中抽取![]() 个,测量这些面包的一项质量指标值,由测量结果得如下频数分布表:
个,测量这些面包的一项质量指标值,由测量结果得如下频数分布表:
质量指标值分组 |
|
|
|
|
|
频数 |
|
|
|
|
|

(1)在相应位置上作出这些数据的频率分布直方图;
(2)估计这种面包质量指标值的平均数![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(3)根据以上抽样调查数据,能否认为该食品厂生产的这种面包符合“质量指标值不低于![]() 的面包至少要占全部面包
的面包至少要占全部面包![]() 的规定?”
的规定?”



