题目内容
6.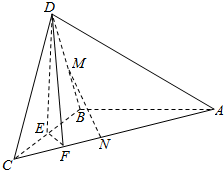 如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC点,F棱AC上,且AF=3FC.
如图,在三棱锥D-ABC中,已知△BCD是正三角形,AB⊥平面BCD,AB=BC=a,E为BC点,F棱AC上,且AF=3FC.(1)求三棱锥D-ABC的体积;
(2)求证:AC⊥平面DEF;
(3)若M为DB中点,N在棱AC上,且CN=$\frac{3}{8}$CA,求证:MN∥平面DEF.
分析 (1)直接利用体积公式,求三棱锥D-ABC的体积;
(2)要证AC⊥平面DEF,先证AC⊥DE,再证AC⊥EF,即可.
(3)M为BD的中点,连CM,设CM∩DE=O,连OF,只要MN∥OF即可.
解答  (1)解:∵△BCD是正三角形,AB⊥平面BCD,AB=BC=a,
(1)解:∵△BCD是正三角形,AB⊥平面BCD,AB=BC=a,
∴三棱锥D-ABC的体积V=$\frac{1}{3}×\frac{\sqrt{3}}{4}{a}^{2}×a$=$\frac{\sqrt{3}}{12}{a}^{3}$.
(2)证明:取AC的中点H,∵AB=BC,∴BH⊥AC.
∵AF=3FC,∴F为CH的中点.
∵E为BC的中点,∴EF∥BH.则EF⊥AC.
∵△BCD是正三角形,∴DE⊥BC.
∵AB⊥平面BCD,∴AB⊥DE.
∵AB∩BC=B,∴DE⊥平面ABC.∴DE⊥AC.
∵DE∩EF=E,∴AC⊥平面DEF.
(3)解:连CM,设CM∩DE=O,连OF.
由条件知,O为△BCD的重心,CO=$\frac{2}{3}$CM.
当CN=$\frac{3}{8}$CA时,CF=$\frac{2}{3}$CN,∴MN∥OF.
∵MN?平面DEF,OF?平面DEF,
∴MN∥平面DEF.
点评 本题考查棱锥的结构特征,证明线面垂直,线面平行,考查体积的计算,考查逻辑思维能力,是中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
18.已知三棱锥A-BCD中,点E,F分别是AB,CD的中点AC=BD=2,且直线AC,BD所成的角为60°,则线段EF的长度为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 1或$\sqrt{2}$ | D. | 1或$\sqrt{3}$ |
15.若一个三棱锥的底面是边长为3的正三角形,高为2$\sqrt{3}$,所有侧棱均相等,则侧棱长为( )
| A. | $\sqrt{21}$ | B. | $\sqrt{15}$ | C. | $\sqrt{3}$ | D. | 1 |
16.设m=a2+a-2,n=2a2-a-1,其中a∈R,则( )
| A. | m>n | B. | m≥n | C. | m<n | D. | m≤n |
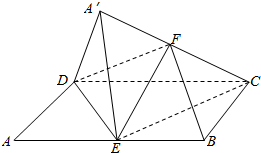 如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°.E为线段AB的中点,将△ADE沿直线DE翻折成△A′DE,使面A′DE⊥平面BCD,F为线段A′C的中点.
如图,在平行四边形ABCD中,AB=2BC,∠ABC=120°.E为线段AB的中点,将△ADE沿直线DE翻折成△A′DE,使面A′DE⊥平面BCD,F为线段A′C的中点.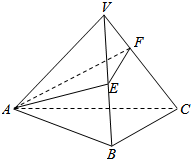 如图,在三棱锥V-ABC中,VA=VB=VC=4,∠AVB=∠AVC=∠BVC=30°,过点A作截面△AEF,求△AEF周长的最小值.
如图,在三棱锥V-ABC中,VA=VB=VC=4,∠AVB=∠AVC=∠BVC=30°,过点A作截面△AEF,求△AEF周长的最小值.